Because $\frac{dy}{dx}$ has killed all the creativity inside!

Geometry Level 3

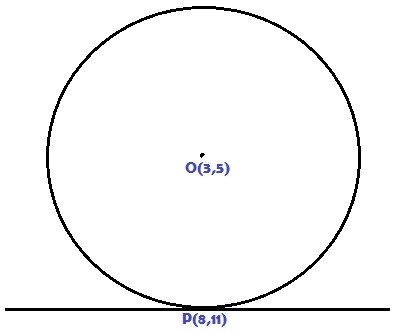
As shown in the figure, a circle centered at $O=(3,5)$ bears a point $P=(8,11)$ hosting a line tangent to the circle. Can you find out the equation of that tangent line without using calculus?

If the equation of the line can be expressed in the form $ax+by+c=0$ , where $a$ , $b$ and $c$ are integers and $\gcd(a,b,c)=1$ , then enter $|abc|$ as your answer.

Notations :

$\gcd(\cdot)$ denotes the greatest common divisor function.
$| \cdot |$ denotes the absolute value function .

The answer is 3180.

1 solution

Md Zuhair
Aug 29, 2016

Now By Our Method without Calculus , We Need The Straight Line Knowledge.

Now the slope of the line $OP$ is $11-5/8-3$ = $6/5$

Now We know that P is a point on the tangent , then $OP$ is the normal of the tangent

Now we know for Perpendicular lines $m_1*m_2= -1.$

Hence Slope of the tangent is $-5/6.$

Now we will put in two point form to get

=> $y-11 / x-8 = -5/6$

Now after solving this equation we get a equation. Now we will compare the equation with $ax+by+c=0$ to get $|abc| = 3180.$

I had posted the solution to this question before, but accidentally deleted it. Thanks for this one bro :D

Arkajyoti Banerjee - 4 years, 9 months ago

No problem.

Md Zuhair - 4 years, 9 months ago

Because d y d x \frac{dy}{dx} d x d y ​ has killed all the creativity inside!

The answer is 3180.

1 solution

0 pending reports

Because $\frac{dy}{dx}$ has killed all the creativity inside!