Behind the Question Mark 2
In the following puzzle, dashed arrows denote addition while solid arrows denote multiplication:
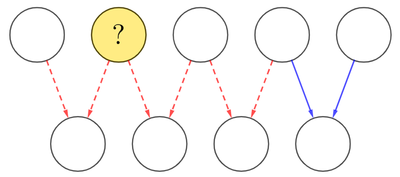
If all circles contain distinct positive integers from to , how many different possible integers replace the question mark?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The 3 multiplicative circles can only be 2,3,6 or 2,4,8 which comply with xy = z < 10 for x ≠ y ≠ z. For 2,3,6, the complementary summative components are {1,4,5,7,8 & 9} with joint collaboration of 2 or 3 for a total sum of 36 or 37 respectively. On the other hand, for 2,4,8, the complementary summative components are {1,3,5,6,7 & 9} with joint collaboration of 2 or 4 for a total sum of 33 or 35 respectively.
In short, we have :
1) sum of {1,4,5,7,8 & 9} + 2 = 36
2) sum of {1,4,5,7,8 & 9} + 3 = 37
3) sum of {1,3,5,6,7 & 9} + 2 = 33
4) sum of {1,3,5,6,7 & 9} + 4 = 35
Looking at 1), obviously 9 should be in one of the lower sum circles but not at the middle one. Why? Because the total is even and the 4 upper summands will have the same total as those of the left and right lower circles as their 2 sums.
36 - (double the sum of upper circles) = (even number at middle lower circle) = {4 or 8}
Since 3 is being placed at the far right upper circle as factors of 6, then 4 by the summation of 1+3 is impossible to be placed at middle lower, leaving 8 to be there. This 8 must be the the sum of 1 and 7 as the only possible summands available within {1,4,5,7,8 & 9}. 9 must have either 1 or 7 as its summand, but 8 is already taken (midlow) so 1+8 is a no go and 7+2 is now confirmed. From the above, 1 must be at the ? circle and be paired with 4 for a sum of 5.
Solution 1 :
4-5-(? = 1)-8-7-9-2-6-3
Looking at 2), using the same arguments as above, midlow must be an odd number with its summands both available among {1,4,5,7,8 & 9}. That could be one of these three possibilities : 1+4=5 or 1+8=9 or 4+5=9. But 8 as a MIDDLE summand is impossible since it's already too large by itself and any other summands paired to it will exceed a sum of 9. And keeping in mind that a 1 must be in an upper circle (it can only be summand and never a sum as the smallest of the bunch), for 4+5=9 a 1 must be paired with either of the summands, but 5 is unavailable being another upper circle and 6 is the 'leader' of the multiplication group. Knowing 5 as the midlow, it's easy to see that ? is again 1 for a Solution 2 as below :
8-9-(? = 1)-5-4-7-3-6-2
Looking at 3), using the same arguments as above, midlow must be an odd number with its summands both available among {1,3,5,6,7 & 9}. That could be one of these two possibilities : 1+6=7 or 3+6=9. Both have a mutual summand of 6 which cannot be paired with the collaborator 2 since 8 is part of another group. Even without solving it fully we already reached the conclusion of ? = 6. Anyway, the Solution 3 is :
1-7-(? = 6)-9-3-5-2-8-4
Looking at 4), using the same arguments as above, midlow must be an odd number with its summands both available among {1,3,5,6,7 & 9}. That could be one of these two possibilities : 1+6=7 or 3+6=9. Both have a mutual summand of 6 which cannot be paired with the collaborator 4 since 10 is a two digits number. Even without solving it fully we already reached the conclusion of ? = 6. Anyway, the Solution 4 is :
3-9-(? = 6)-7-1-5-4-8-2
Conclusion : ? = 1 or ? = 6.
Answer = 2 different positive integers.