Behold the power of the sun!
Solar collector power generation plants, such as this one in Spain, work by concentrating solar energy into a small region to drive a steam turbine.
Direct sunlight delivers about 1 0 0 0 Watts/m 2 of energy in the infrared, visible, and ultraviolet parts of the spectrum. I want to use mirrors with a total effective area A to direct this solar energy into a cube 1 m on a side, heating the cube to a steady 1 0 0 ∘ Celsius so I can start generating steam and running a turbine. What is the necessary effective mirror surface area A in m 2 to do this?
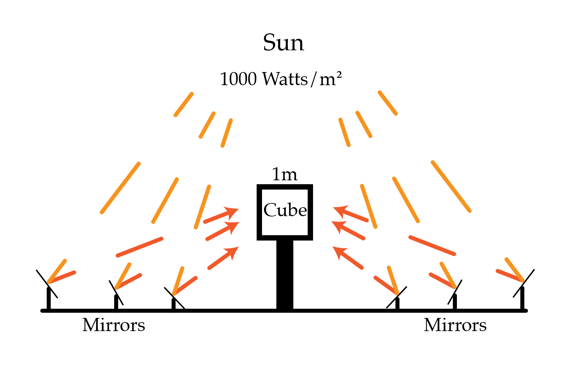
Note that your A will be smaller than you might expect. This is because we have used components that are 100% efficient - all the solar energy gets directed onto the cube. In a real life situation the amount of solar energy redirected by the mirrors is much, much less.
Details and assumptions
- The cube absorbs and emits as a perfect blackbody. It's well insulated so you can ignore any conductive or convective heat transfer.
- The air around the cube is 2 0 ∘ Celsius.
- You don't need to worry about any energy lost turning the water into steam. You just want to get the cube up to the specified temperature. (In a real turbine this additional energy loss would need to be taken into account.)
- Effective area takes into account the angle of the mirrors with respect to the sun, so when calculating the effective area you can ignore the orientation of the mirrors. If the mirrors are angled, the true surface area is larger than the effective area.
The answer is 4.083.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
12 solutions
The heat delivered by the radiation is equal to the surface area of the cube (i.e. 6m^2) times the difference between (i) the heat emitted by the black body which as per Stefan-Boltzmann is a constant times the temperature to the power of four (the temperature has to be expressed in degrees Kelvin, ie 373K) minus (ii) the heat absorbed calculated in similar manner but using the exterior temperature (i.e. 293k).
A Power loss from radiation can be calculated as:
P = ε σ ( T 4 − T a 4 ) A c
ε = emissivity of the object (When it is a blackbody, ε=1)
σ=Stefan-Boltzmann constant
Ac=Area of the cube
T=temperature of the cube (Always in kelvin) Ta= temperature of the air around the cube
So lets find P, that is the power:
P = ε σ ( T 4 − T a 4 ) A c
P = 1 ∗ 5 . 6 7 0 ∗ 1 0 − 8 ∗ ( 3 7 3 4 − 2 9 3 4 ) ∗ 6
P ≈ 4 0 7 8 W
So, finally:
1 0 0 0 = A P
A = 4 , 0 7 8 m 2
use T=373.15 instead of 373 to get the more accurate result.
Doesn't this assume the air is a black body radiator?
The energy absorbed by the cube is: P i n = p A + σ T 2 4 S .
The energy emitted by the cube is: P o u t = σ T 1 4 S
Where p = 1 0 0 0 W / m 2 , σ is Stefan–Boltzmann constant, T 1 = 3 7 3 K , T 2 = 2 9 3 K , S = 6 m 2 is the total surface area of the cube.
P i n = P o u t , so A = p σ S ( T 1 4 − T 2 4 ) = 4 . 0 8 ( m 2 ) .
Whats pA here?
From the Stefan–Boltzmann law and cube is a perfect back body so we have equation about the balance between solar energy and energy of thermal radiation :
σ.( T 1 4 - T 2 4 ) . S = 1000. A
σ is the Stefan–Boltzmann constant, σ ≈ 5.67 × 10−8 W/(m2K4)
T 1 : a steady absolute temperature at 100+273= 373 K
T 2 : the ambient absolute temperature at 20 +273 = 293 K
S : the toal area of the cube's surface , S= 6.1.1= 6 m 2
finally we calculate the value of A which is the essentially efficient mirror area :
A ≈ 4.078 m 2 ( the incredible figure when efficiency is 100% )
Since we can ignore convective or conductive heat transfer, the only way the cube will lose energy is due to radiation into the surrounding area. The power loss due to radiation is given by P=A cσϵ(T 4−T 40), where A c is the surface area of the cube, σ is the Stefan-Boltzmann constant, ϵ is the emissivity, T is the temperature of the cube and T_0 is the temperature of the air. Note that you cannot neglect the temperature of the air in this problem! Also, as a fun aside, the energy loss rate scaling as the temperature of the object to the fourth power is one of the reasons you feel 'cold' when you have a fever. Our body is actually sensitive to the rate of energy loss, so when you have a fever you lose energy more quickly and feel cold.Returning to our problem, since the cube is a perfect blackbody, ϵ(emissivity)=1 and we can then calculate a total power loss of 4083 Watts. This loss must be compensated for by the energy coming in from the mirrors, and so the total area of the mirrors is 4.083 m^2.
sorry the math is not looking good but i can be understood all right ..
The heat delivered by the radiation is equal to the surface area of the cube (i.e. 6m^2) times the difference between (i) the heat emitted by the black body which as per Stefan-Boltzmann is a constant times the temperature to the power of four (the temperature has to be expressed in degrees Kelvin, ie 373K) minus (ii) the heat absorbed calculated in similar manner but using the exterior temperature (i.e. 293k).
The cube reaches radiation equilibrium when net radiation leaving the surface is equal to the net radiation entering the surface Radiation entering the cube is equal to = 1000 watt/ m^3 x effective area Radiation leaving the cube is give. By stefans law on thermal radiation σ = 5.670373(21)×10−8 W m−2 K−4.[1] = X. ( T^(4) ) Here it is equal to σ ( T^(4) - t^(4)) Where T = 100 deg celcius = 373 K And t = 20 degree celcius = 293 K So A_eff x 1000 = σ ( T^(4) - t^(4)) Substituting the values we get the answer
Since we can ignore conductive and convective heat transfer,the only way the cube will lose energy is owing to radiation into the surrounding area.The power loss due to radiation is given by P=(Surface Area of the Cube) * (The Stefan-Boltzman Constant) * (The emissivity of the body) * (The temperature of the cube ^ 4) * (The temperature of the air). =4081 watts.(as the emissivity of the black body = 1) This loss needs to be compensated the energy supplied by the mirrors from the sun. Thus the total effective area of the mirrors=P / (power supplied by the sun per unit area) =4081 / 1000 square metre = 4.081 square metre.
The power loss from radiation is P = A c σ ϵ ⋅ ( T 4 − T 0 4 ) , where A c is the surface area of the cube and the others are constants and temperatures. Since the cube is a perfect blackbody, ϵ = 1 . We find that the total power loss is 4 . 0 8 × 1 0 3 W and so the area is 4 . 0 8 m 2 .
Heat lost by thermal radiation: P= \sigma (T_{cube}^4 - T_{surrounding}^4) *S_{total} = 4078 W Power by the sun equals to heat loss: 1000 A=4078, A=4.078 m^2
We apply the Stefan - Boltzmann formula to calculate the radiating power of the cube: P = A ε σ ( T 4 − T e 4 ) where, A is the area of the cube, so A = 6 m 2 (the cube has 6 faces of 1 m 2 ). ε is emmissivity, ε = 1 for perfect blackbody. σ = 5 . 6 7 × 1 0 − 8 J s − 1 m − 2 K − 4 is the Stefan - Boltzmann constant. And T and T e is the temperature in Kelvin of the cube and environment respectively, so T = 3 7 3 K and T e = 2 9 3 K . Apply the numbers, we have P = 4 0 8 3 W . This power must be equal to the supplied power from the collector. So the necessary effective area of collector is: A = P / 1 0 0 0 = 4 0 8 3 / 1 0 0 0 = 4 . 0 8 3 m 2
Stefan's Law states that the intensity of thermal radiation emitte by a black body is I = σ T 4 . Where σ = 5 . 6 7 ⋅ 1 0 − 8 m 2 K 4 W is Stefan-Boltzmann constant and T is the absolute temperature of the cube. For the cube to have a constant temperature, the rate of absorbed energy flowing to the cube must be the same as emitted energy. The absorbed energy comes from the sun ray deflected by the mirrors of effective area A . Hence,
W a b s o r b e d = W e m i t t e d
I s u n A = σ ( T c u b e 4 − T a i r 4 ) A c u b e
A c u b e = 6 m 2 is the surface area of the cube. Inputting the given quantities, we get A = 4 . 0 8 3 m 2