Being odd is fun

Relevant wiki: Stars and Bars

Since $x_1, x_2, x_3$ are odd positive integers, we can write them as $x_1=2a+1,x_2=2b+1,x_1=2c+1$ for non-negative integers $a,b,c$ . We then look for the number of solutions to the equation $a+b+c=24$ which, by Stars and Bars, gives us $325$ .

$x_{1}+x_{2}+x_{3} = 51$

Let us denote all the possible values of the variables $x_1$ , $x_2$ and $x_3$ as powers of $x$ and Multiply the possible values of all the variables. We want the Sum of variables to be equal to $51$ . Which means we are trying to find coefficient of $x^{51}$ . Using formula of G.P we will simplify the expression.

$x^1+x^3+x^{5}+\cdots+x^{47}+x^{49}$

$\underbrace{(x^1+x^3+x^{5}+\cdots+x^{49} )\cdot(x^1+x^3+x^{5}+\cdots+x^{49} )\cdot (x^1+x^3+x^{5}+\cdots+x^{49} )}_{3 \text{ times because 3 variables }}$

$x^3(x^0+x^2+x^{4}+\cdots+x^{48})^{3} \hspace{5mm} \small\text{ coeff of } x^{51} \\ (x^0+x^2+x^{4}+\cdots+x^{48})^{3} \hspace{9mm} \small\text{ coeff of } x^{48} \\ \left(\dfrac{1-x^{51}}{1-x^2}\right)^{3} \hspace{2mm} = \hspace{2mm} \underbrace{(1-x^{51})^{3}}_{\small\text{expansion does not contain coeff of }x^{48} } \times (1-x^2)^{-3}$

Now

$\begin{aligned} \dfrac{1}{1-x^2} & = \displaystyle\sum_{r=0}^{\infty}x^{2r} \\ \dfrac{(-1)(-2x)}{(1-x^2)^{2}} & = \displaystyle\sum_{r=0}^{\infty}(2r)x^{2r-1} \\ \dfrac{1}{(1-x^2)^{2}} & = \displaystyle\sum_{r=0}^{\infty}(r)x^{2r-2} \\ \dfrac{(-2)(-2x)}{(1-x^2)^{3}} & = \displaystyle\sum_{r=0}^{\infty}(r)(2r-2)x^{2r-3} \\ \dfrac{1}{(1-x^2)^{3}} & = \displaystyle\sum_{r=0}^{\infty}\dfrac{(r)(r-1)}{2}x^{2r-4} \\ 2r-4 & = 48 \hspace{8mm} r = 26 \end{aligned}$

Coefficient of $x^{48}$ = $\dfrac{26 \times 25 }{2} = \boxed{325}$

---

This is the idea behind Stars and Bars Method , in short @Grant Bulaong solution is ideal .

Since $x_1, x_2,$ and $x_3$ are odd positive integers, write each as $x_i = 2n_i + 1$ for non-negative integers ${n_i}, i=1, 2, 3$ . Then the total number of triplets $(x_1, x_2, x_3)$ satisfying $x_1 + x_2 + x_3 = K$ for odd positive integer $K$ is the same as the number of triplets satisfying $n_1 + n_2 + n_3 = N$ where $N = \frac{1}{2}(K-3)$ . For our problem, $K=51$ and $N=24$ .

To count the number of triplets $(n_1, n_2, n_3)$ , regard the equation $n_1 + n_2 + n_3 = N$ as a family of line segments in the first quadrant of the $(n_1,n_2)$ -plane, each having a slope -1 and parameterized by its intercept of $c = N-n_3$ with the axes: $n_1 + n_2 = c, c\in{0, ..., N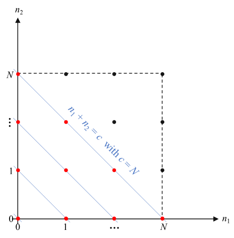}$ . For each line segment, we seek all non-negative solutions for its given parameter value $c\in{0, ..., N}$ . Each such segment contains $c+1$ solutions (e.g., see figure). All possible solutions consist of the integral lattice points on and below the diagonal $n_1 + n_2 = N$ of an $(N+1)\times(N+1)$ square of such points. The number of solution points on the diagonal is $N+1$ . The number off the diagonal is $\frac{1}{2}[(N+1)^2-(N+1)]$ (where the factor of $\frac{1}{2}$ is to count only non- diagonal points below the diagonal), so the total number of integral solutions is: $\frac{1}{2}[(N+1)^2-(N+1)] + (N+1) = \frac{1}{2}[(N+1)^2+(N+1)] = \frac{1}{2}(N+1)(N+2)$ .

For $N=24$ , the total number of solutions is: $\frac{1}{2}(25)(26) = 25\cdot13 = 325$ . ANSWER: $\boxed{325}$

Note: This is also a way to see that $\displaystyle \sum_{k=1}^n k = \frac{1}{2}n(n+1)$ .