Bending backwards

Classical Mechanics Level 4

A cold-rolled strip of sheet metal is sometimes delivered rolled up in a tight coil. When the coil is left to relax freely the strip of metal does not spring back to a flat shape; instead it has a residual curvature, see the photo below. It may take a rather strong force to straighten it out, and if left alone it will coil back to the original shape.

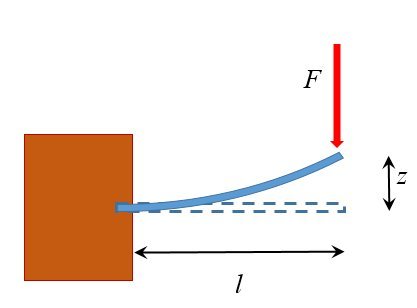
First, we we want to characterize the elastic strength of the strip. We cut out a small piece and measure the elasticity of the strip by a method illustrated in the next Figure. One end of the strip is clamped so that the clamped part is horizontal and the rest of the strip curves upward. A force $F$ is exerted from the top down at the other end of the the strip until it becomes, in a good approximation, straight. The length of the free standing strip is $l$ , and the measured displacement of the end is $z_0$ . (We set up this experiment so that $z<<l$ ). Clearly, the more resistant is the strip the larger force is needed to straighten it out.

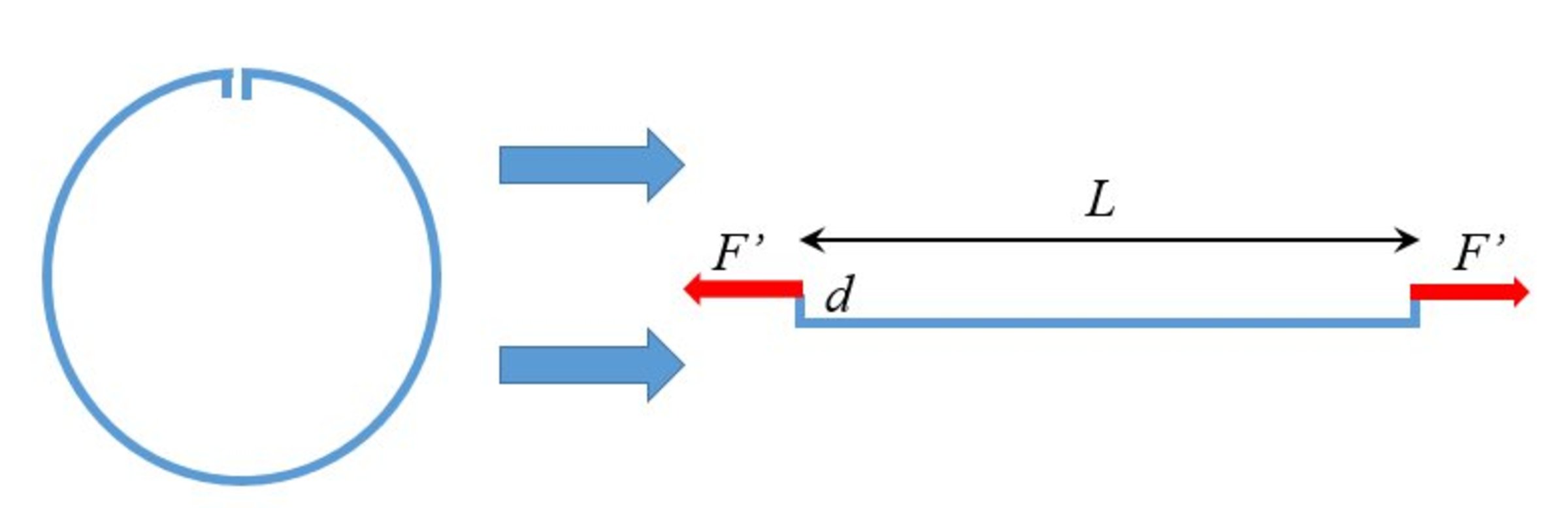
Next we take a long piece of the strip in such a way that it makes a full circle when it is un-stressed. Using strong pliers we make $90^{\circ}$ bends at the ends, as illustrated in the Figure below. The whole length of the strip is $L$ and the bent pieces have a length of $d$ . After all of this is done, and the strip is left alone, the two ends of the strip barely touch each other (see the left side of the Figure below).

Now we straighten the strip by pulling the edges of the bent pieces with forces of magnitude $F'$ in opposite directions (see the right side of the Figure below). What is the magnitude of $F'$ ? Enter the answer in Newtons, to 3 significant digits.

Numbers: $F=2.0N$ , $l=5.0cm$ , $z_0=0.5cm$ , $L=0.50m$ , $d=1.5cm$ .

The answer is 13.95.

1 solution

Laszlo Mihaly
Sep 26, 2017

The fundamental equation describing the bending of the strip is

$\frac{1}{R}= \frac{\tau}{A}$

Here $R$ is the radius of curvature, $\tau$ is the torque and $A= Y I$ , where $Y$ is the Young's modulus and $I$ depends on the cross sectional shape and dimensions of the material. This equation is usually applied to flat shapes ( $1/R=0$ ) that bend under the influence of the applied torque, but we can equally well apply the same approach in the current problem.

For the first part we can write the curvature as $1/R = z''/(1+z'^2)^{3/2} \approx z''$ , where $z(x)$ is the deflection of the strip as a function of the distance from the clamped end, $x$ , and the approximation holds as long as $z'<<1$ or $z_0<<l$ . The torque is $\tau= (l-x)F$ . Solving the differential equation $z''= (l-x)F/A$ yields

$z_0= F L^3/3A$ .

When we pull out the strip as described in the problem we exert a torque of $\tau=F'd$ that is independent of the position along the strip. This is very important as it makes it possible for the whole strip to be straight. The original radius of curvature was $R=L/2 \pi$ . Using $\frac{1}{R}= \frac{\tau}{A}$ again we get

$1/R = dF'/A$

Expressing $A$ from the second equation, we get

$F'=\frac{2 \pi}{3} \frac{Fl^3}{z_0 L d} = 13.95N$

Bending backwards

The answer is 13.95.

1 solution

0 pending reports