Bent Wire Moment

Classical Mechanics Level 2

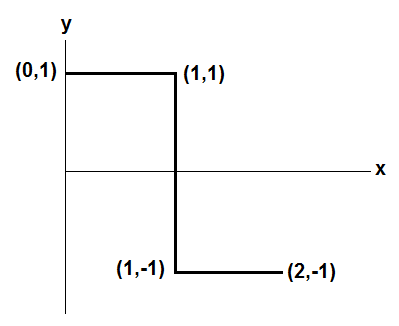
A bent wire of mass $M$ has the geometry shown above. The wire's moment of inertia with respect to the $y$ -axis can be expressed as:

$\large{I_y = \frac{A}{B} M}$

If $A$ and $B$ are co-prime positive integers, what is $A + B$ ?

Note: The wire's mass is uniformly distributed over its length

The answer is 13.

2 solutions

Andre Bourque
Jul 18, 2018

I solved it in a similar way to Steven Chase, by doing cases on the segments. However, I don't know any formulas so I applied the integration definition of moment of inertia for case 1 and 3, case 2 is a constant radius of 1 so it's just the mass.

I also used numerical integration as a double-check. Fewer abstractions involved that way

Steven Chase - 2 years, 10 months ago

Steven Chase
Jul 10, 2018

Segment #1 (horizontal): Use moment formula for rod about end
Segment #2 (vertical): Equivalent to a single point-mass
Segment #3 (horizontal): Use moment formula for rod about center and use parallel axis theorem

Segment #1:

$\large{I_{y 1} = \frac{M}{4} \frac{1^2}{3} = \frac{M}{12} = \frac{4 M}{48}}$

Segment #2:

$\large{I_{y 2} = \frac{M}{2} 1^2 = \frac{24 M}{48}}$

Segment #3:

$\large{I_{y 3} = \frac{M}{4} \frac{1^2}{12} + \frac{M}{4} \Big (\frac{3}{2} \Big )^2 = \frac{M}{48} + \frac{9 M}{16} = \frac{28 M}{48}}$

Total Moment:

$\large{I_{y} = I_{y 1} + I_{y 2} + I_{y 3} = \frac{4 M}{48} + \frac{24 M}{48} + \frac{28 M}{48} =\frac{56 M}{48} = \frac{7}{6} M}$

Bent Wire Moment

The answer is 13.

2 solutions

0 pending reports