Berry Barter

Algebra Level 3

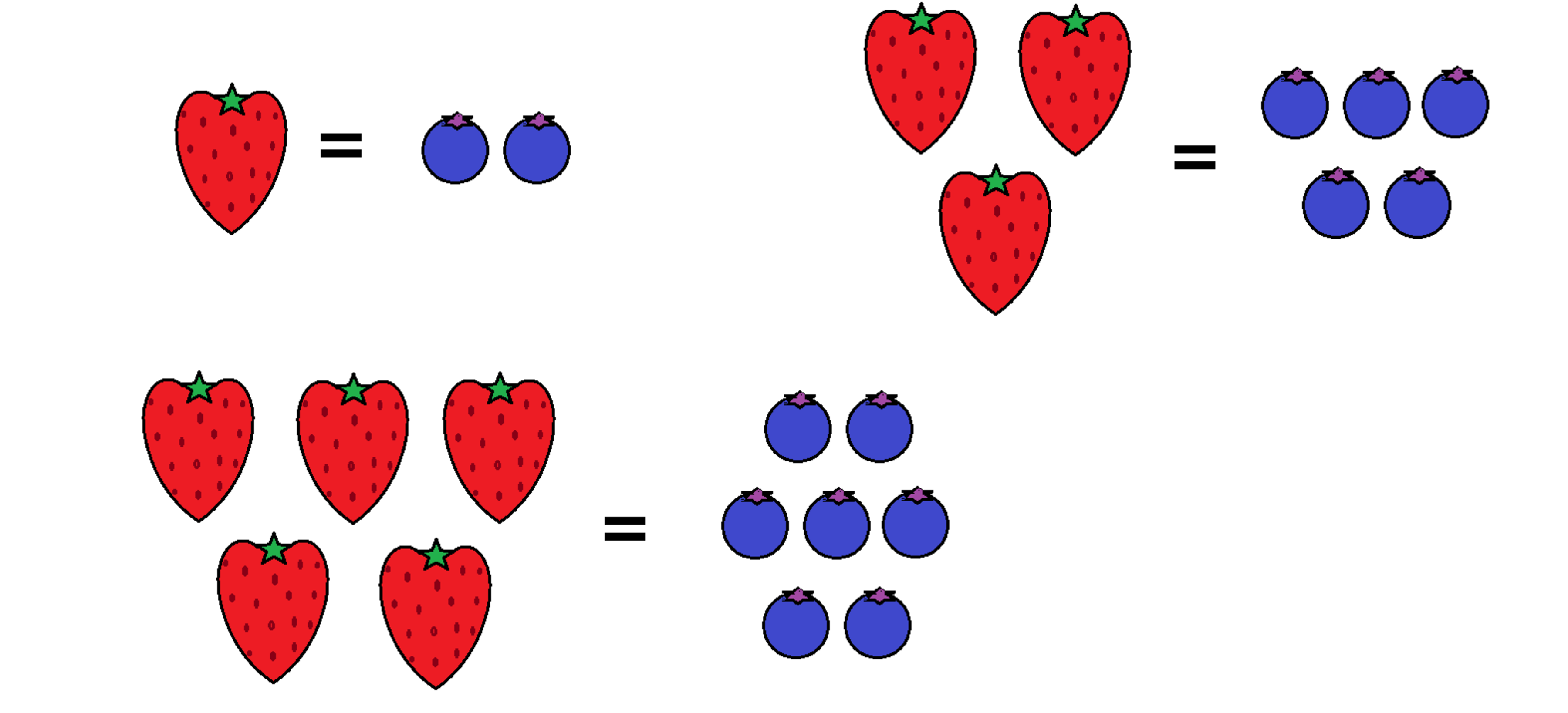
You have a strawberry farm next to your neighbor's blueberry farm. During the harvest season, you and your neighbor will exchange the goods in friendly barters as shown above: 1 strawberry for 2 blueberries, 3 strawberries for 5 blueberries, and 5 strawberries for 7 blueberries.

Over the last season, you gave your neighbor 36 strawberries and got 59 blueberries in return. If the number of trades for all three types of barters are all in prime numbers, how many times did you trade in total?

The answer is 14.

1 solution

Worranat Pakornrat
Oct 10, 2016

Let $x$ be the number of trades for the first barter, $y$ be the number of trades for the second barter, and $z$ be be the number of trades for the third barter.

Then from the strawberry farm, the number of given strawberries will be: $36 = x + 3y + 5z$ .

And for the blueberry farm, the traded blueberries will be: $59 = 2x + 5y + 7z$ .

Multiplying $2$ for the first equation, we will get: $72 = 2x + 6y + 10z$ .

Subtracting from the second equation: $13 = y + 3z$ .

Since $x, y, z$ are all prime, $z$ can only be $2$ or $3$ as the value over $3$ will result in negative $y$ .

If $z = 2$ , then $y = 7$ , but if $z = 3$ , then $y = 4$ , which is not satisfying the condition.

Therefore, $z = 2$ , $y = 7$ , and $x = 5$ .

Checking the answers: $36 = 5 + 3\cdot 7 + 5\cdot 2$ and $59 = 2\cdot 5 + 5\cdot 7 + 7\cdot 2$ . All work well.

As a result, the total number of trades = $5 + 7 + 2 = \boxed{14}$ .

Berry Barter

The answer is 14.

1 solution

0 pending reports