Best Illumination
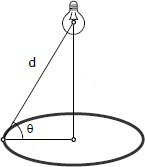
A light is to be placed above the center of a circular area. What ratio of the height of the light to the radius of the area gives the best illumination on a circular walk surrounding the area?
We need to use the fact that the intensity of illumination for a single source is directly proportional to the sine of the angle of incidence and inversely proportional to the square of the distance from the source.
The answer is 0.707107.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let h be the height of the light and r the radius of the illuminated area. If I is the intensity of illumination, we are told that I ∼ d 2 sin θ = d 3 h = ( h 2 + r 2 ) 3 / 2 h Therefore I will be maximized when the right hand side of the above equation is maximized. Setting the derivative of that expression equal to zero yields d h d ( h 2 + r 2 ) 3 / 2 h ( h 2 + r 2 ) 3 ( h 2 + r 2 ) 3 / 2 − 3 h 2 ( h 2 + r 2 ) 1 / 2 ( h 2 + r 2 ) − 3 h 2 2 h 2 h = 0 = 0 = 0 = r 2 = 2 r Multiply through by ( h 2 + r 2 ) 5 / 2 h and r are both positive All that remains is to find the ratio of the height to the radius: r h = 2 1 ≈ 0 . 7 0 7 1