Bet You Never Thought About This

At the risk of being redundant, I just thought it would help to generate a general formula for the area of a triangle given its altitudes.

In general, let the side lengths of a triangle be $a,b,c$ and the respective altitudes from these sides be $h_{a}, h_{b}, h_{c}.$ Then with $A$ being the area of the triangle, we have that

$2A = ah_{a} = bh_{b} = ch_{c} \Longrightarrow a = \dfrac{2A}{h_{a}}, b = \dfrac{2A}{h_{b}}, c = \dfrac{2A}{h_{c}}.$

Now using Heron's formula $A = \sqrt{s(s - a)(s - b)(s - c)}$ where $s = \dfrac{a + b + c}{2}$ , we can substitute in our expressions for $a,b,c$ and simplify to get the area of the triangle, (in inverse form), exclusively in terms of the altitudes, i.e.,

$\dfrac{1}{A} = \sqrt{\left(\dfrac{1}{h_{a}} + \dfrac{1}{h_{b}} + \dfrac{1}{h_{c}}\right)\left(\dfrac{1}{h_{a}} + \dfrac{1}{h_{b}} - \dfrac{1}{h_{c}}\right)\left(\dfrac{1}{h_{a}} + \dfrac{1}{h_{c}} - \dfrac{1}{h_{b}}\right)\left(\dfrac{1}{h_{b}} + \dfrac{1}{h_{c}} - \dfrac{1}{h_{a}}\right)}.$

Plugging in $h_{a} = 3, h_{b} = 4, h_{c} = 5$ , we find that

$\dfrac{1}{A} = \dfrac{\sqrt{47*23*17*7}}{60^{2}} \Longrightarrow A = \dfrac{3600\sqrt{128639}}{128639},$

and so $a + b = 3600 + 128639 = \boxed{132239}.$

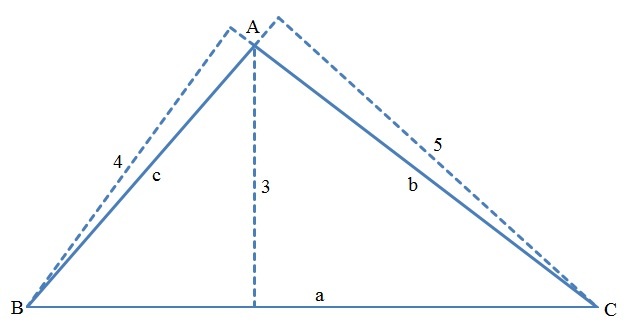
Let the triangle be $\triangle ABC$ with respective side lengths $a$ , $b$ and $c$ . The altitude from $A$ , $B$ and $C$ be $3$ , $4$ and $5$ respectively. Then the area of $\triangle ABC$ is given by:

$A_\triangle = \frac{1}{2}(3a) = \frac{1}{2}(4b) = \frac{1}{2}(5c) \quad \Rightarrow b = \frac{3}{4}a \quad \Rightarrow c = \frac{3}{5}a$

From Heron's formula, we have, $A_\triangle = \sqrt{s(s-a)(s-b)(s-c)}$ , where $s=\frac{1}{2}(a+b+c) = \frac{1}{2} (1+\frac{3}{4}+\frac{3}{5})a = \frac{47}{40}a$ .

$\Rightarrow \sqrt{s(s-a)(s-b)(s-c)} = \dfrac {3a}{2} \quad \Rightarrow \sqrt{\frac{47}{40}\times \frac{7}{40}\times \frac{17}{40}\times \frac{23}{40}}a^2 = \dfrac{3a}{2} \\ \Rightarrow \sqrt{128639} a = 2400 \quad \Rightarrow a = \dfrac {2400}{\sqrt{128639}}$

$A_\triangle = \dfrac {3a}{2} = \dfrac {3\times 2400}{2\sqrt{128639}} = \dfrac {3600\sqrt{128639}}{128639}$

$\Rightarrow a+b = 3600+128639 = \boxed{132239}$

Let the area of the triangle be $A$ . The sides of the triangle are then $\frac{2A}{3}$ , $\frac{2A}{4}$ and $\frac{2A}{5}$

Using the cosine rule, and cancelling the common factor $(2A)^2$ , the smallest angle (which will be opposite the smallest side) satisfies

$cos(\theta)=\dfrac{\frac{1}{9}+\frac{1}{16}-\frac{1}{25}}{2\times\frac{1}{3}\times \frac{1}{4}}=\frac{481}{600}$

From this it follows that

$sin(\theta)=\dfrac{\sqrt{128639}}{600}$

Now writing down the area of the triangle in terms of two sides and the included angle gives

$A=\frac{1}{2}\times \frac{2A}{3}\times \frac{2A}{4}\times \dfrac{\sqrt{128639}}{600}$

Solving this for $A$ gives

$A=\dfrac{3600}{\sqrt{128639}}=\dfrac{3600\sqrt{128639}}{128639}$

and the result follows.

I wrestled with this for a whole day, and the woke up with the idea that the sides of the triangle must be in the ratio $\frac{1}{3}:\frac{1}{4}:\frac{1}{5}$ , so that they give the same result (twice the area) when multiplied by the corresponding perpendicular sides.

The solution then almost wrote itself.