Better not stop pedaling
Between doing physics problems on Brilliant, some people like to unicycle. A unicyclist is cycling up a hill angled with respect to the horizontal. The center of mass of the cyclist is directly over the axle of the wheel and the cyclist/unicycle system have a combined mass of The radius of the wheel is and the coefficient of static friction between the wheel and the asphalt is
What is the magnitude of the torque (in
) that the cyclist needs to exert on the pedals in order to cycle up the hill at a constant speed?
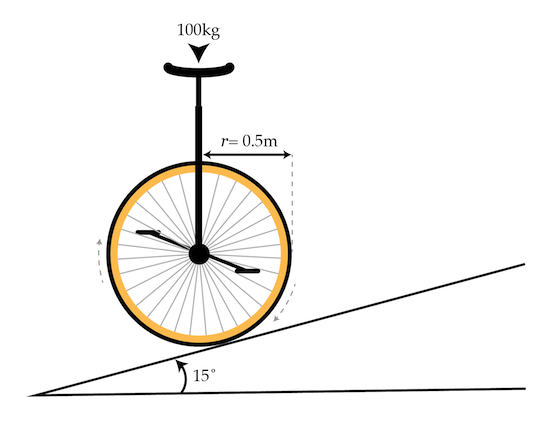
Details and assumptions
- The unicycle does not slip against the hill.
- You may take the acceleration of gravity to be
- You may neglect air resistance.
The answer is 126.821.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
If we have our unicycle on flat ground, it exerts a force m g on the ground below. When the plane is tilted at an angle θ , the normal force become F N = μ m g cos θ . Similarly, the force along the plane is given by F ∥ = m g sin θ .
In order for the unicycle to remain at a given height, it must exert a force equal in magnitude to F ∥ up the plane. The force due to the torque τ is given by F τ R so that F τ = τ / R .
Equating this with the force down the plane, we have F τ = τ / R = m g sin θ .
Thus we find τ = m g R sin θ .
Note, this is the magnitude of the force up the plane, but the force is provided by the normal force. Thus, it must be the case that F τ m g sin θ tan θ ≤ F N ≤ μ m g cos θ ≤ μ . So that θ max = arctan μ . Above this level of incline, the unicycle could not proceed up the incline. For μ = 1 , this corresponds to θ = 4 5 ° .