Vigilant Triangle(s)
Consider a right triangle A B C with ∠ C = 9 0 ∘ . Suppose that the hypotenuse A B being divided into four equal parts by the points D , E , F , such that A D = D E = E F = F B . If C D 2 + C E 2 + C F 2 = 3 5 0 . What is the length of A B ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Thanks very much, Sir. By the way, how do I fix the level of this question?
Log in to reply
It will be automatically adjusted by the system when more people try the problem.
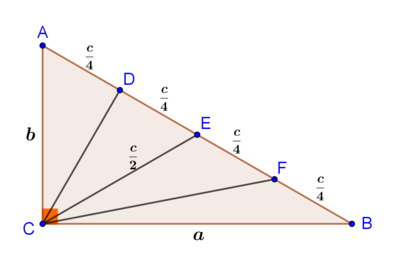 Denote the lengths of
A
B
,
B
C
,
C
A
by
c
,
a
and
b
. Then,
A
D
=
D
E
=
E
F
=
F
B
=
4
c
.
Denote the lengths of
A
B
,
B
C
,
C
A
by
c
,
a
and
b
. Then,
A
D
=
D
E
=
E
F
=
F
B
=
4
c
.
By Pythagorean theorem on △ A B C , c 2 = a 2 + b 2 ( 1 ) Moreover, for the mediean C E of the right △ A B C it holds C E = 2 A B = 2 c Using Apollonius’s theorem on △ C A E and △ C E B we have:
C A 2 + C E 2 = 2 C D 2 + 2 A E 2 ⇒ b 2 + 4 c 2 = 2 C D 2 + 8 c 2 C E 2 + C B 2 = 2 C F 2 + 2 E B 2 ⇒ 4 c 2 + a 2 = 2 C F 2 + 8 c 2 Adding and rearranging,
2 ( C D 2 + C E 2 + C F 2 ) = a 2 + b 2 + 2 3 c 2 ⇒ ( 1 ) 2 × 3 5 0 = 4 7 c 2 ⇒ c 2 = 4 0 0 ⇒ c = 2 0
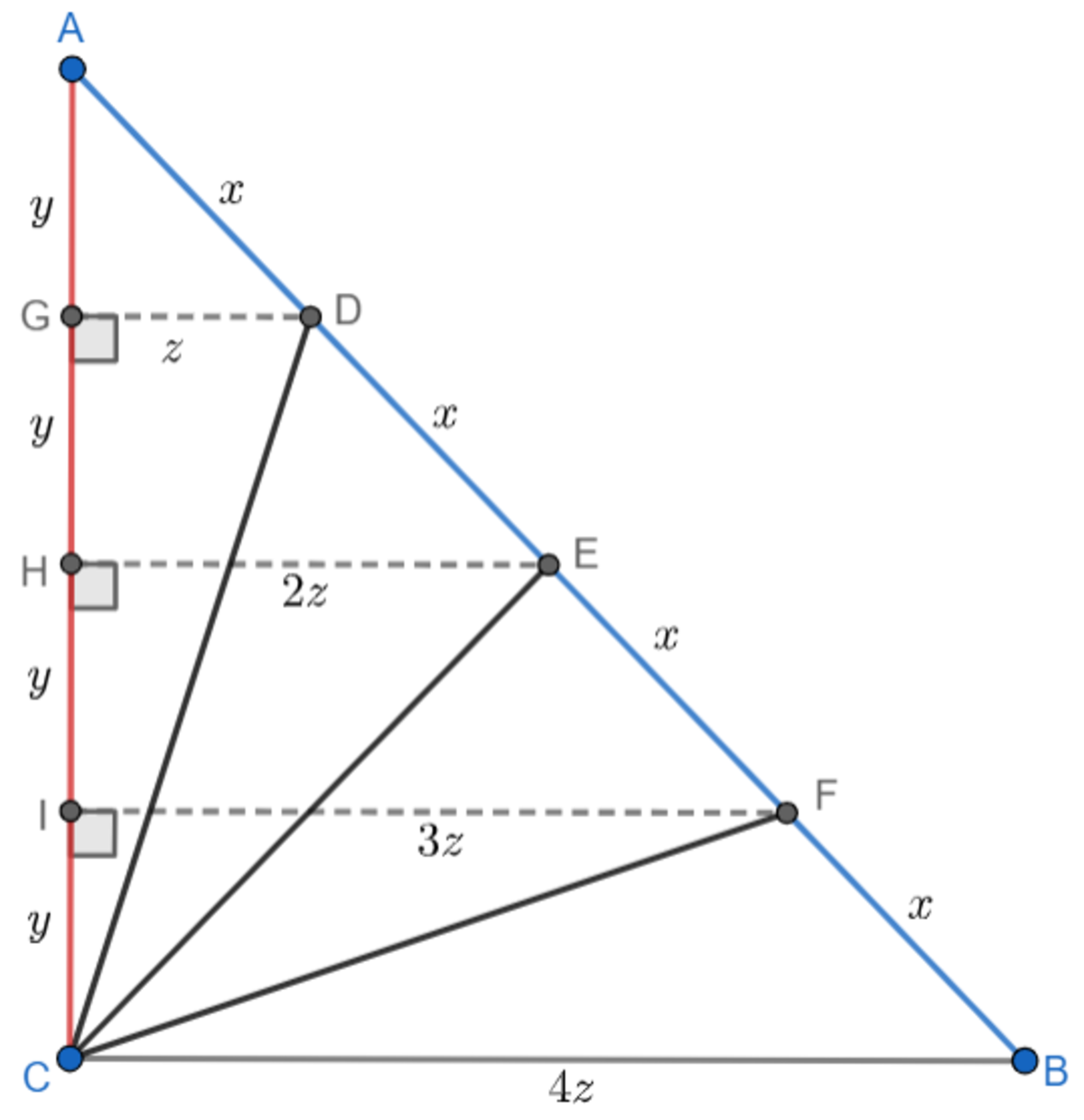
Let A D = D E = E F = F B = x and draw lines through D , E and F parallel to base B C . Let them intersect A C at G , H and I respectively. Since the triangles formed are similar, A G = G H = H I = I C = y D G = z , E H = 2 z , F I = 3 z , B C = 4 z
Using the Pythagorean Theorem in △ C G D , △ C H E and △ C I F , 9 y 2 + z 2 4 y 2 + 4 z 2 y 2 + 9 z 2 = C D 2 = C E 2 = C F 2 Adding the above equations, 1 4 y 2 + 1 4 z 2 = C D 2 + C E 2 + C F 2 = 3 5 0 ⟹ y 2 + z 2 = 2 5 In right-triangle A B C , A C 2 + B C 2 = A B 2 ⟹ A B = 1 6 y 2 + 1 6 z 2 = 1 6 ⋅ 2 5 = 2 0
Really Great Solution. Well, for instance, could you tell me how did you arrive at the similarity of those triangles?
Log in to reply
Thank you.
△ A G D ∼ △ A H E ∼ △ A I F ∼ △ A C B because all of their angles are equal ( ∠ A is common and all are right triangles).
Hope it helps :)
Thanks for your Reply. By the way, there's a small error C E 2 = 4 y 2 + 4 z 2
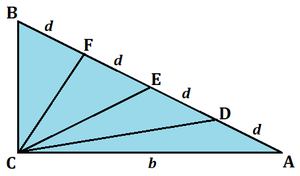
By the law of cosines on △ D A C , C D 2 = d 2 + b 2 − 2 b d cos A .
By the law of cosines on △ E A C , C E 2 = 4 d 2 + b 2 − 4 b d cos A .
By the law of cosines on △ F A C , C F 2 = 9 d 2 + b 2 − 6 b d cos A .
By right △ B A C , b = 4 d cos A .
Adding the first three equations and substituting b = d cos A , C D 2 + C E 2 + C F 2 = 1 4 d 2 + 3 b 2 − 1 2 b d cos A = 1 4 d 2 + 3 b 2 − 3 b 2 = 1 4 d 2 = 3 5 0 .
Therefore, d = 5 and A B = 4 d = 4 ⋅ 5 = 2 0 .
Put C at the origin, A on the y -axis and B on the x -axis. Letting the sides of the triangle be a = B C , b = C A , c = A B as usual, the coordinates of the points are
| A ( 0 , b ) | B ( a , 0 ) | C ( 0 , 0 ) |
| D ( 4 a , 4 3 b ) | E ( 2 a , 2 b ) | F ( 4 3 a , 4 b ) |
so that C D 2 + C E 2 + C F 2 = 1 6 1 [ a 2 + 9 b 2 + 4 a 2 + 4 b 2 + 9 a 2 + b 2 ] = 8 7 [ a 2 + b 2 ]
Since we're told in the question that this is 3 5 0 , and since a 2 + b 2 = c 2 , we find c 2 = 4 0 0
so the length of the hypotenuse is 2 0 .
Let B C = 4 w , A C = 4 h , and C ( 0 , 0 ) be the origin of the x y -plane. Then the coordinates of the other points are A ( 0 , 4 h ) , B ( 4 w , 0 ) , D ( w , 3 h ) , E ( 2 w , 2 h ) , and F ( 3 w , h ) . Then we have:
C D 2 + C E 2 + C F 2 ( w 2 + 9 h 2 ) + ( 4 w 2 + 4 h 2 ) + ( 9 w 2 + h 2 ) 1 4 ( w 2 + h 2 ) ⟹ w 2 + h 2 = 3 5 0 = 3 5 0 = 3 5 0 = 2 5
And A B = B C 2 + A C 2 = 1 6 w 2 + 1 6 h 2 = 1 6 × 2 5 = 2 0 .