Between $9$ and $n$ is a huge difference!

Since $-1 \le a_i \le 1$ for all $i$ , $\left( a_i - \frac{1}{2} \right)^2 (a_i + 1) \ge 0.$ This expands as $a_i^3 - \frac{3}{4} a_i + \frac{1}{4} \ge 0.$ Summing over $1 \le i \le 9$ , we get $-\frac{3}{4} \sum_{i = 1}^9 a_i + \frac{9}{4} \ge 0.$ Therefore, $\sum_{i = 1}^9 a_i \le 3.$

Equality occurs when one of the $a_i$ is equal to $-1$ , and the other eight are equal to 1/2.

If we write $a_j = \cos x_j$ for each $j$ , we want to maximize $f(\mathbf{x}) \; = \; \sum_{j=1}^9 \cos x_j$ subject to the criterion $g(\mathbf{x}) \; = \; \sum_{j=1}^9 \cos^3 x_j \; = \; 0$ Using the method of Lagrange multipliers, at an extremal point we must be able to find $\lambda$ such that $\frac{\partial f}{\partial x_j} - \lambda \frac{\partial g}{\partial x_j} \; = \; -\sin x_j(1 - 3\lambda \cos^2x_j) \; = \; 0$ for each $j$ . Thus we must be able to find some $-1 \le u \le 1$ such that $\cos x_j \in \{1,-1,u,-u\}$ for all $j$ . Thus we must be able to find integers $a,b,c,d \ge 0$ such that $a+b+c+d=9$ and $f \; = \; a - b + (c - d)u \hspace{2cm} g \; = \; a - b + (c - d)u^3 \; = \; 0$ (so, at the extremal point, $a$ of the $\cos x_j$ are equal to $1$ , $b$ are equal to $-1$ , $c$ are equal to $u$ and $d$ are equal to $-u$ . This implies that $|a-b| \le |c-d|$ and that $u \,= \, -\left(\tfrac{a-b}{c-d}\right)^{\frac13}$ .

Thus we need to maximise the expression $F(a,b,c,d) \; =\; (a - b)^{\frac13}\left[(a - b)^{\frac23} - (c - d)^{\frac23}\right]$ over all $4$ -tuples $(a,b,c,d)$ of non-negative integers such that $a+b+c+d = 9$ and $|a-b| \le |c-d|$ . There are $110$ such $4$ -tuples, and it is easy to check that $F$ is maximized at $(0,1,8,0)$ , and the maximum value of $F$ is $\boxed{3}$ .

We first relax the constraint that there are exactly 9 values, and allow for the weighted average of several distinct values.

Consider the graph $y = x^3$ . We want to place several points such that the sum of the y-coordinates is 0, and hence the average is 0, while trying to maximize the x-intercept, and hence their average.

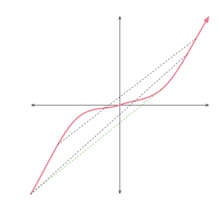
If the $a_i$ consisted of 2 distinct values, then the visual image is as follows:
Consider all pairs of points on the curve, and draw the connecting line segment. Then, the place where this connecting line cuts the x-axis will give us a weighted average (with positive weights, have yet to determine the exact weights, or guarantee if we can have an integer number of them) such that the sum of the y-coordinates is 0, and we can determine the corresponding x-intercept.

What happens if we have 3 or more distinct values? The equivalent idea is to take the convex hull of these points, which gives us the set of possible values where, with suitably determined positive weights, we can get the corresponding averages. However, taking the convex hull of these points gets potentially hard to generalize.
To simplify this idea, note that we can simply take the line segments which intersect the x-axis, and we know that the intersection of the convex hull with the x-axis must lie within the points determined by these line segments.

As such, this ultimately reduces to:

Take any line segment with endpoints on the graph $y = x^3, -1 \leq 0 \leq 1$ . What is the maximum possible x-intercept of these line segments?

Visually, it should not be hard to convince yourself that we want one point at $(-1,-1)$ , and the other point such that the line segment is tangential to the curve. This is the green line. Note: With some thought, you can see how this motivate's Jon's first inequality of $\left( a_i - \frac{1}{2} \right)^2 (a_i + 1) \ge 0.$

For completely, let's do this properly using coordinate geometry. Suppose that the line segment has endpoints $( -a, -a^3), ( b, b^3 )$ with $0 \leq a, b \leq 1$ . The line between these 2 points satisfies

$\frac{ y + a^3 } { x + a } = \frac{ b^3 + a^3 } { b + a }$

The $x-$ intercept occurs when $y = 0$ , hence is equal to $x^* = - a + \frac{ a^3 } { a^2 - ab + b^2 }$ . For a fixed value of $a$ , to maximize this value, we want to minimize $a^2 - ab + b^2$ , which happens when $b = \frac{a}{2}$ . For this value of $b$ , we get $x^* = \frac{a}{3}$ . Thus, the maximum value of the x-intercept is $\frac{1}{3}$ . We know that we want to use the points $(-1, -1), ( \frac{1}{2} , \frac{1}{8} )$ .

We now deal with the initial constraint relaxation. It is clear to see that the maximum value can indeed be achieved by taking the weights 1 and 8, which sum to the 9, as required in the problem.