Beware the Mine Squares!
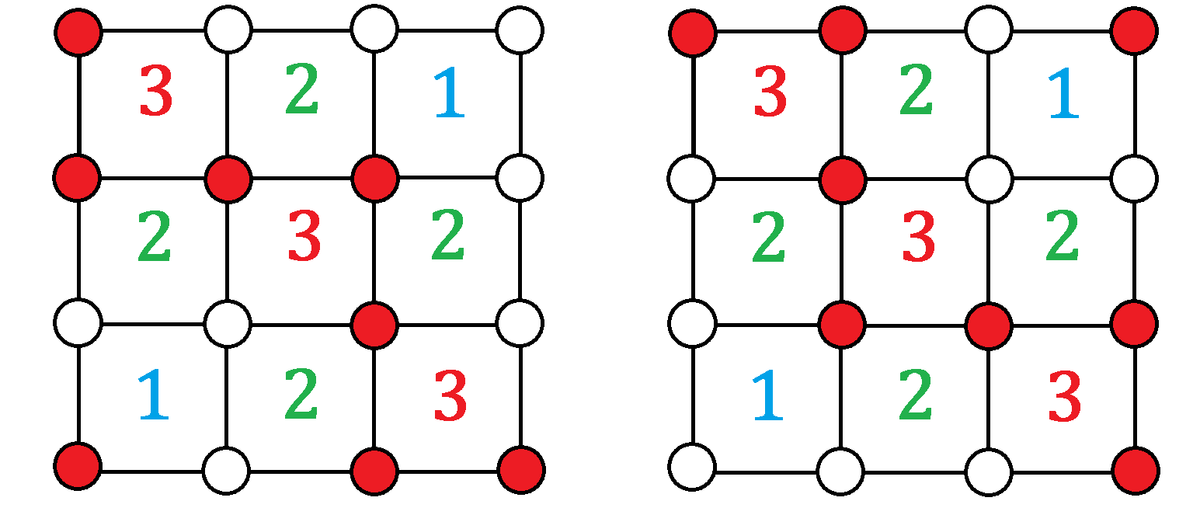
Each of the nodes--the small circles--of the squares below may or may not have a bomb. The number in each square indicates the number of bombs planted around that square.
How many nodes have bombs?
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
It's great that you recognized "I am leaving off is an existence proof" :)
Very clever
whatever are you talking about?
Log in to reply
Hi Stephen - that was my first reaction as well. But please take some time to think about Bradley's solution because it does make sense! One little hint - if there are 16 'cells' what could they possibly be?
He says that you can get the exact count by adding the four numbers in the four corner squares of the 3 x 3 grid. Every one of the sixteen possible mine locations is a corner of exactly one of these four squares.
Very nice :D
Very nice approach!
Consider the 3-square bomb at either corner, 3 out of 4 nodes must have the bombs, leaving one free.
Now we choose the free node to be at the big square's corner, the adjacent 2-squares will be automatically occupied with 2 bombs each. However, since the center square's number is 3, at least one more bomb must be placed in either territory, making it contradicted. Thus, the free node can't be at the far corner.
Then, for generality, if the free node is the one shared between the lower right 3-square and the center 3-square territory, that will leave the rest of the nodes of the center to have bombs and consequently making the adjacent 2-squares at middle upper and left middle to be occupied. However, the 3-square at the upper left will still need a place to plant bomb on either of the 2-squares, making it again contradicted.
Hence, the free node must be in other corner, and that will lead to these combinations:
With reflection, there are 2 possible ways to plant the bombs according to the numbers, resulting in 8 bombs in total.
Moderator note:
This problem is a slight variant of traditional Minesweeper. When given a traditional Minesweeper configuration, just asking "is an answer possible?" is known as the Minesweeper Consistency Problem . It is known to be NP-complete (NP stands for "Non-deterministic Polynomial"). Roughly, this indicates that there is no known algorithm that can resolve a arbitrary large Minesweeper Consistency Problem in a reasonable time.
If a polynomial-time algorithm was ever discovered to solve the Minesweeper Consistency Problem, this would be equivalent to proving P = NP and would resolve one of the Millennium Prize Problems .
Interesting that there are multiple ways to place the bombs.
How can one arrive at these configurations?
Log in to reply
I've put some basic ideas behind planting the bombs into my solution. I hope it will be useful.
Log in to reply
Great! Considering the diagonal of 3-squares allows us to determine most of the bomb placement. Since 3/4 of the circles are filled, that is extremely restrictive, hence it makes sense for us to begin considering form there.
these two possibilities are actually one, these are not different, you can obtain another by just rotating the picture. the structure is not different.
very perfect answer thanks.
One key leading to the solution is to realize the symmetry in the way the numbers are dispersed.
Log in to reply
Except that the solution is not symmetric the way the numbers are. The numbers are symmetric around either diagonal axis, but the solution is only symmetric around 1.
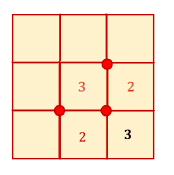
 The central
3
can be done in only two ways (the other two being effectively the same due to symmetry of the problem).
The central
3
can be done in only two ways (the other two being effectively the same due to symmetry of the problem).
The two alternatives are shown using the red bombs.
The one on top works for the two red 2 ’s shown, but then it fails for the black 3 as there is no way to add two more bombs.
So the second arrangement is the only one possible.
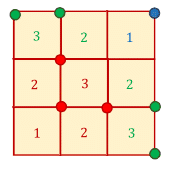
Once that’s decided, every remaining placement of a bomb is forced by the numbers.
The two red 2 ’s and the red 1 are satisfied by the first three bombs.
The two green 3 ’s require the green bombs to be added.
Now the green 2 ’s are full up.
The blue 1 is the only one left, and one blue bomb in the corner will take care of that.
Counting the bombs, there are 3 red, 4 green, and 1 blue, that is 8 total.
I thought it will be a very nasty case check. This method eliminates all cases, great!
I like this approach because starting with the central square forces all of the rest of the decisions.
The total number of bombs are 6 + 7 +6 = 19 The total number of circles are 4 x 4 =16 So 19 >16 do not see why each circle could not have at least one bomb? Now, when you make the arrangement it is unclear what the condition is?! You may overlap, but I do not see how the nods (cercles) could not be assigned all with a bomb in.
Log in to reply
The idea is the old mine sweeper computer game. Each node with a bomb is counted into all four of the numbers surrounding it. So one bomb in one of the nodes inside is counted four times, one bomb in one on the edge is counted twice, and the one in the corner just once.
not so useful very confusing
Consider the four squares that encompass all sixteen nodes, without overlapping. You do not need to know which specific nodes have bombs because you know the total from each of these four squares (3, 1, 1, and 3) for a total of
8
.
Four Squares
Original & clean!
Bradley's solution with a picture added.
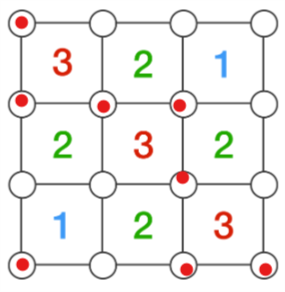 it is just like playing minesweeper, the hints that show you how many bombs are there, are actually useful when you figure out the boxes which are not bombed. This is a classic problem of elimination and deduction. Just like Enstein's riddle.
it is just like playing minesweeper, the hints that show you how many bombs are there, are actually useful when you figure out the boxes which are not bombed. This is a classic problem of elimination and deduction. Just like Enstein's riddle.
There are still available bombs and free nodes. The provide solution seems double count bombs in square into node
not 2 ways there is one more way to solve it
I found the following to be simple and direct.
Start with the center 3. There are 4 ways to fill it.
Place bombs in (2,2) and (3,3) adjacent 3-square corners.
Place a bomb in (3,2) . (2,3) is equivalent and produces a reflection of the solution below.
Placing bombs in both (2,3) and (3,2) will fail so there are only the two possible choices above.
Placing bombs in (2,2), (3,3) and (3,2) eliminates a few nodes.
(2,3) (3-square has 3)
(2,1) and (3,1) (2-square has 2)
(4,2) and (4,3) (2-square has 2)
(4,1) (1 square has 1)
3 filled, 6 eliminated by force.
Bombs must go into (1,1) and 1,2) to satisfy the corner 3-square. The eliminates (1,3) (2-square has 2)
Bombs must go into (3,4) and (4,4) to satisfy the corner 3-square. The eliminates (2,4) (2-square has 2)
7 filled, 8 eliminated by force.
This leaves only a bomb in (1,4) to satisfy the 1-square and account for all 16 nodes.
All forced once the initial state of the center 3 is fixed.
Thus 8 is the unique answer found in two symmetrical solutions depending on the initial choice of node adjoining a 1-coner from the center 3-square.
Oh woah, I didn't thought that it's possible to solve this by starting from the middle cell. I thought we must start with the corner 1's.
This certainly works. Thanks.
I added the numbers in the 4 corners together..
Why does that work? Are you sure there exists a solution?
There are a total of 16 cells. The 3 by 3 grid of numbers, each number indicates the total bombs for the four cells surrounding it. The corner numbers each give the total of the four cells around them. There is no overlap, and they account for every cell. Add up the four corner numbers (3 + 1 + 1 + 3). That should be the answer if the numbers are possible. The only possibility I am leaving off is an existence proof. It is possible but pointless for the numbers to indicate an impossible configuration that could never be satisfied by all the numbers. Putting some faith in the problem writer, I did one quick mental check that made me believe it was possible, but I did not write it down and may have lacked rigor.