Bézout's Bicentric Brilliance

Geometry Level 5

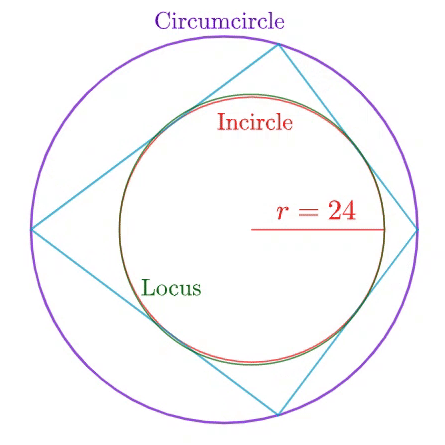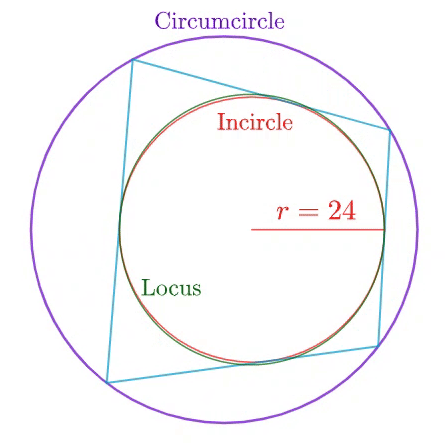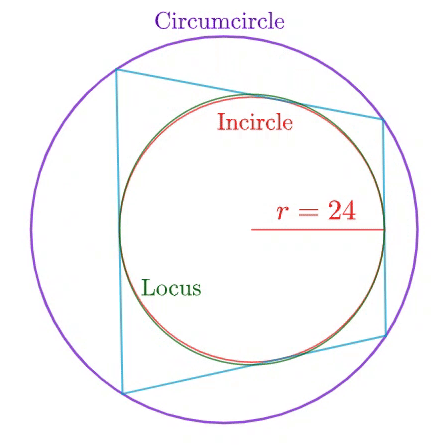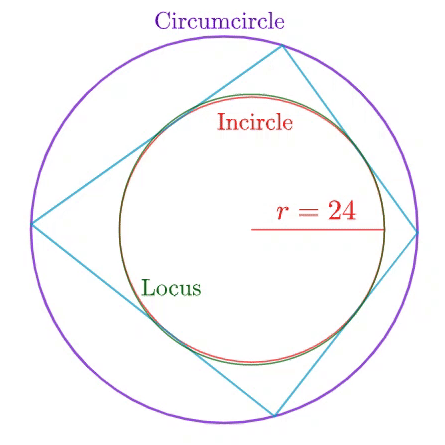
Four vertices on the circumference of a circumcircle of radius $35$ altogether form a bicentric quadrilateral whose inradius (in red) is $24$ . As those vertices vary, the poristic locus of the four midpoints on their respective sides of the quadrilateral forms an elegant curve (in green). It can be shown that

$\dfrac{\text{area of the incircle}}{\text{area enclosed by the locus}} = \dfrac{A}{B}$

where $A$ and $B$ are coprime positive integers. Find the value of $A + B$ .

Note. As the animation appears cluttered, here is the "cleaner" version of the animation above.

The answer is 2329.

1 solution

Yuriy Kazakov
May 16, 2021

From Kerawala 1947 (39) $d=5$ for $R=35$ and $r=24$ .

Two circles

$x^2+y^2=24^2$

$(x-5)^2+y^2=35^2$

Midpoint locus

$x(t)=24 \cos{t}+5 \sin^2{t}$

$y(t)=24 \sin{t}-5 \sin{t} \cos{t}$

Locus Area

$\large\int^{2 \pi}_0 \frac{x'(t)y(t)-x(t)y'(t)}{2} dt =1177\pi$

and Circle Area $24^2\pi=1152 \pi$ give answer $1152+1177 =2329$ .

Slight error here... The locus area is $\int_0^{2\pi}\tfrac12(x'(t)y(t) - x(t)y'(t))\,dt = \tfrac{1177}{2}\pi$ and the incircle area is $24^2\pi = 576\pi$ . The ratio of these areas is then $\frac{2\times576}{1177} = \frac{1152}{1177}$ , giving us the answer.

Mark Hennings - 3 weeks, 6 days ago

Thanks. My error on the way from paper to monitor...

Yuriy Kazakov - 3 weeks, 6 days ago

Bézout's Bicentric Brilliance

The answer is 2329.

1 solution

0 pending reports