Twice as Normal
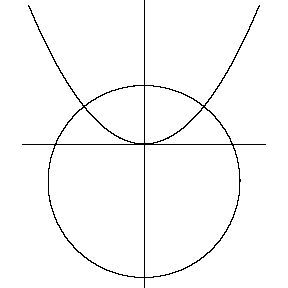
A circle of radius 1 whose center is on the -axis is normal to the parabola as shown in the figure above. Find the -coordinate axis displacement from the center of the circle.
Give the answer to 5 decimal places.
The answer is 0.39039.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The parabola equation is y 1 = x 2 while the circle equation (the upper part) is y 2 = 1 − x 2 + c , being c the y coordinate of the circle center.
In the intersection point, the intersection is normal. That means that d x d y 1 = d x d y 2 − 1 . Or:
2 x = 1 − x 2 − x − 1
2 x 2 = 1 − x 2
4 x 4 + x − 1 = 0
Solving for bhaskara, and since the intersection point iss both a solution for the parabola and the circle x 2 = y = 0 . 3 9 0 3 8 8 2 0 3 . . . and x = 0 . 6 2 4 8 1 0 5 3 4 . . .
Pluggin this in the circle equation y 2 = 1 − x 2 + c leads to c = − 0 . 3 9 0 3 8 8 2 0 3 . Since the displacement is the absolut value, out answer is 0 . 3 9 0 3 8 8 2 0 3