Big bases
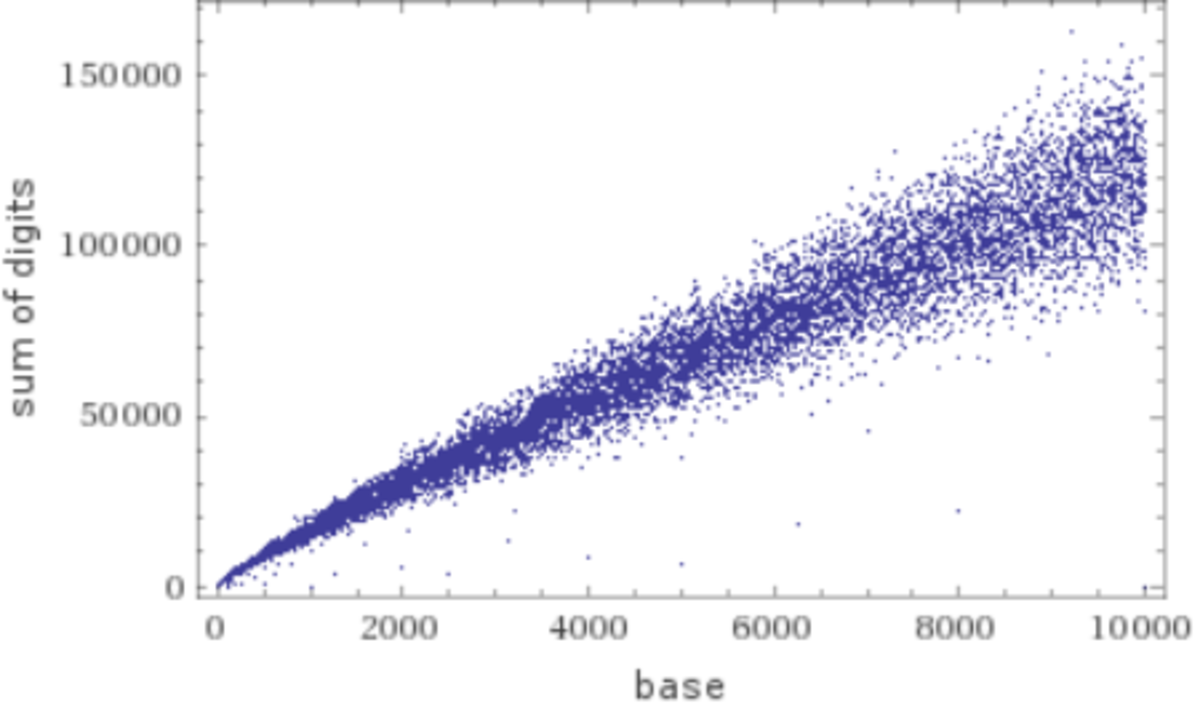
A huge 100 digit number N is written out in every base from 2 to 10,000. What can we say about the digit sum of N as the base increases? (We are looking for a general trend, there may be specific counter examples.)
For example, if N=22, in base 10, the digit sum is 2+2=4. In base 2, however, it is 10110, so the digit sum is 1+0+1+1+0=3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Base 2: the length of the number is about l o g 2 ( 1 0 1 0 0 ) , and each digit averages at (0+1)/2. So the digit sum should be near l o g 2 ( 1 0 1 0 0 ) / 2 = 1 0 0 l o g 2 ( 1 0 ) / 2 .
Base 3: The length of the number is l o g 3 ( 1 0 1 0 0 ) , and each digit averages at ( 0 + 1 + 2 ) / 3 = 1 . So the digit sum should be near 1 0 0 l o g 3 ( 1 0 ) .
Base N: The length of the number is l o g N ( 1 0 1 0 0 ) , and each digit averages at N ( N − 1 ) / ( 2 N ) = ( N − 1 ) / 2 . So the digit sum should be near 1 0 0 ( N − 1 ) l o g N ( 1 0 ) / 2 = ( 5 0 l n ( 1 0 ) ) ( N − 1 ) / l n ( N ) .
Since N-1 grows faster than l n ( N ) , the digit sum is generally increasing.
Graph of digit sum of 10^100: http://www.wolframalpha.com/input/?i=digit+sum+of+googol+in+base+2&lk=2