Big circle, right angles, isosceles triangle

Geometry Level 4

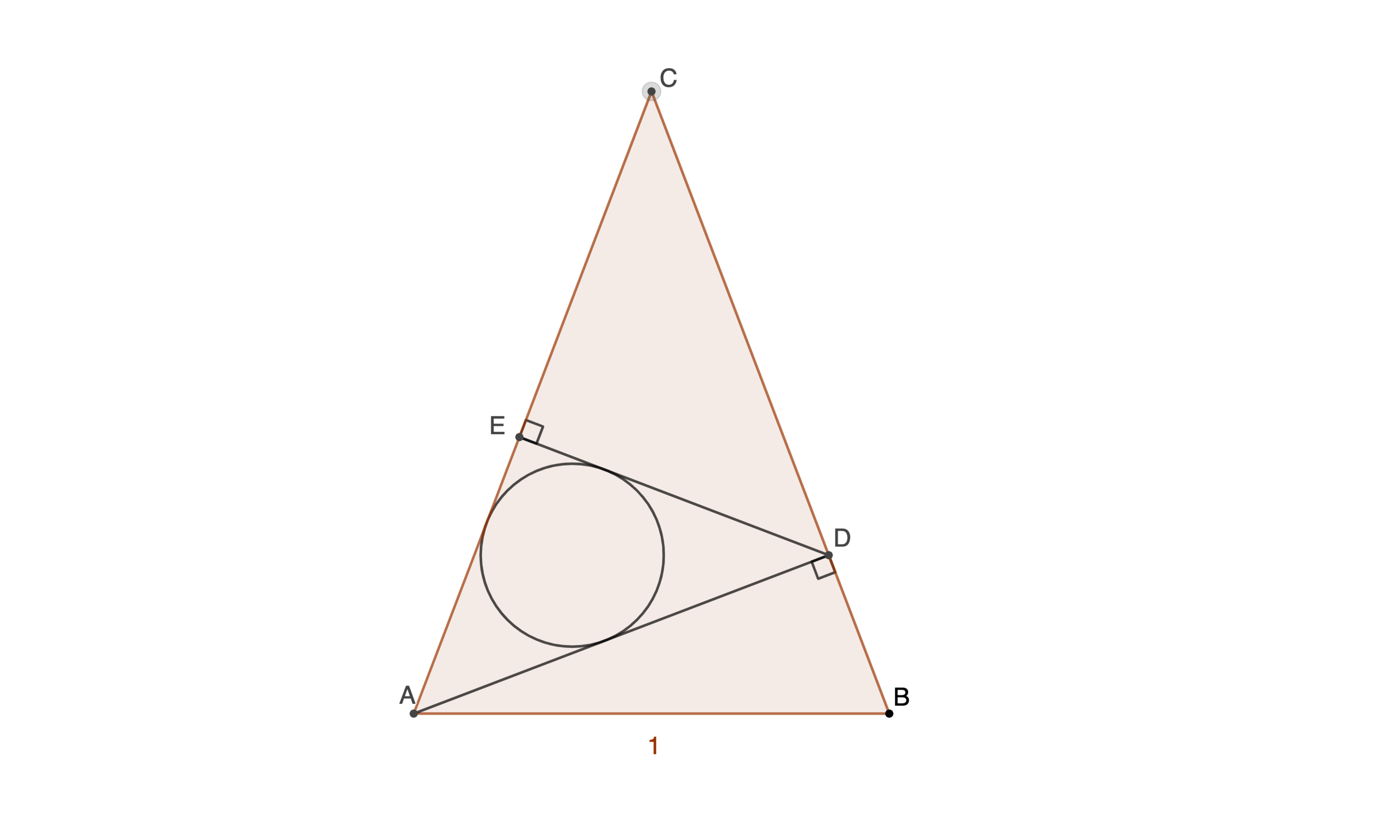
△ A B C \triangle ABC is an isosceles triangle with a base length of 1 1 . A D ⊥ C B AD \perp CB and E D ⊥ A C ED \perp AC . E E is chosen to maximize the radius, r r , of the incircle of △ A D E \triangle ADE . If r = p q r = \dfrac{\sqrt p}{q} , where p p and q q are positive integers and p p is square-free, submit p + q p+q .


The answer is 12.

Fletcher Mattox by Fletcher Mattox , 72, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Let ∠ A C B = 2 θ \angle ACB = 2 \theta . Let M M be the center of the circle and N N its point of contact with A C AC . Then
∠ D A B = 90 ∘ − ∠ D B A = 90 ∘ − 180 ∘ − ∠ A C B 2 = 90 ∘ − 180 ∘ − 2 θ 2 = θ \angle DAB=90{}^\circ -\angle DBA=90{}^\circ -\dfrac{180{}^\circ -\angle ACB}{2}=90{}^\circ -\dfrac{180{}^\circ -2\theta }{2}=\theta Hence, A D = A B cos ⁡ θ ⇒ A D = cos ⁡ θ AD=AB\cos \theta \Rightarrow AD=\cos \theta Consequently,

A E = A D cos ⁡ ( 90 ∘ − 2 θ ) ⇒ A E = cos ⁡ θ ⋅ sin ⁡ ( 2 θ ) ( 1 ) AE=AD\cos \left( 90{}^\circ -2\theta \right)\Rightarrow AE=\cos \theta \cdot \sin \left( 2\theta \right) \ \ \ \ \ (1) Moreover,

∠ N A M = ∠ C A D 2 = 90 ∘ − 2 θ 2 = 45 ∘ − θ \angle NAM=\dfrac{\angle CAD}{2}=\dfrac{90{}^\circ -2\theta }{2}=45{}^\circ -\theta Hence,

A E = A N + N E = r cot ⁡ ( 45 ∘ − θ ) + r ⇒ A E = r ( cot ⁡ ( 45 ∘ − θ ) + 1 ) ( 2 ) AE=AN+NE=r\cot \left( 45{}^\circ -\theta \right)+r\Rightarrow AE=r\left( \cot \left( 45{}^\circ -\theta \right)+1 \right) \ \ \ \ \ (2) Combining ( 1 ) (1) and ( 2 ) (2) we have a function for r r w.r.t. θ \theta :

r ( cot ⁡ ( 45 ∘ − θ ) + 1 ) = cos ⁡ θ ⋅ sin ⁡ ( 2 θ ) ⇔ r = cos ⁡ θ ⋅ sin ⁡ ( 2 θ ) cot ⁡ ( 45 ∘ − θ ) + 1 = 2 sin ⁡ θ cos ⁡ 2 θ cot ⁡ θ + 1 cot ⁡ θ − 1 + 1 = 2 sin ⁡ θ cos ⁡ 2 θ 2 cot ⁡ θ cot ⁡ θ − 1 = sin ⁡ θ cos ⁡ 2 θ cos ⁡ θ sin ⁡ θ cos ⁡ θ sin ⁡ θ − 1 ⇔ r = sin ⁡ θ cos ⁡ θ ( cos ⁡ θ − sin ⁡ θ ) ⇔ r = 2 2 sin ⁡ 2 θ sin ⁡ ( 45 ∘ − θ ) , θ ∈ ( 0 ∘ , 90 ∘ ) \begin{aligned} & r\left( \cot \left( 45{}^\circ -\theta \right)+1 \right)=\cos \theta \cdot \sin \left( 2\theta \right) \\ & \Leftrightarrow r=\dfrac{\cos \theta \cdot \sin \left( 2\theta \right)}{\cot \left( 45{}^\circ -\theta \right)+1}=\dfrac{2\sin \theta {{\cos }^{2}}\theta }{\dfrac{\cot \theta +1}{\cot \theta -1}+1}=\dfrac{2\sin \theta {{\cos }^{2}}\theta }{\dfrac{2\cot \theta }{\cot \theta -1}}=\dfrac{\sin \theta {{\cos }^{2}}\theta }{\dfrac{\dfrac{\cos \theta }{\sin \theta }}{\dfrac{\cos \theta }{\sin \theta }-1}} \\ & \Leftrightarrow r=\sin \theta \cos \theta \left( \cos \theta -\sin \theta \right) \\ & \Leftrightarrow r=\dfrac{\sqrt{2}}{2}\sin 2\theta \sin \left( 45{}^\circ -\theta \right) ,\quad \theta \in \left( 0{}^\circ ,90{}^\circ \right) \\ \end{aligned} Taking the derivative

d r d θ = 0 ⇔ 2 2 [ 2 cos ⁡ ( 2 θ ) sin ⁡ ( 45 ∘ − θ ) − sin ⁡ ( 2 θ ) cos ⁡ ( 45 ∘ − θ ) ] = 0 ⇔ 2 cos ⁡ ( 2 θ ) sin ⁡ ( 45 ∘ − θ ) = sin ⁡ ( 2 θ ) cos ⁡ ( 45 ∘ − θ ) ⇔ 2 tan ⁡ ( 45 ∘ − θ ) = tan ⁡ ( 2 θ ) ⇔ 2 1 − tan ⁡ θ 1 − tan ⁡ θ = 2 tan ⁡ θ 1 − tan ⁡ 2 θ ⇔ tan ⁡ 2 θ − 3 tan ⁡ θ + 1 = 0 ⇔ tan ⁡ θ = 3 ± 5 2 θ = tan ⁡ − 1 ( 3 ± 5 2 ) \begin{aligned} \dfrac{dr}{d\theta }=0 & \Leftrightarrow \dfrac{\sqrt{2}}{2}\left[ 2\cos \left( 2\theta \right)\sin \left( 45{}^\circ -\theta \right)-\sin \left( 2\theta \right)\cos \left( 45{}^\circ -\theta \right) \right]=0 \\ & \Leftrightarrow 2\cos \left( 2\theta \right)\sin \left( 45{}^\circ -\theta \right)=\sin \left( 2\theta \right)\cos \left( 45{}^\circ -\theta \right) \\ & \Leftrightarrow 2\tan \left( 45{}^\circ -\theta \right)=\tan \left( 2\theta \right) \\ & \Leftrightarrow 2\dfrac{1-\tan \theta }{1-\tan \theta }=\dfrac{2\tan \theta }{1-{{\tan }^{2}}\theta } \\ & \Leftrightarrow {{\tan }^{2}}\theta -3\tan \theta +1=0 \\ & \Leftrightarrow \tan \theta =\dfrac{3\pm \sqrt{5}}{2} \\ & \theta ={{\tan }^{-1}}\left( \dfrac{3\pm \sqrt{5}}{2} \right) \\ \end{aligned} Studying the sign of the derivative we see that r ( θ ) r\left( \theta \right) has a maximum at θ = θ 0 = tan ⁡ − 1 ( 3 − 5 2 ) \theta ={{\theta }_{0}}={{\tan }^{-1}}\left( \dfrac{3-\sqrt{5}}{2} \right) .

For this value of θ \theta we have

r = sin ⁡ θ 0 cos ⁡ θ 0 ( cos ⁡ θ 0 − sin ⁡ θ 0 ) = tan ⁡ θ 0 1 + tan ⁡ 2 θ 0 ⋅ 1 1 + tan ⁡ 2 θ 0 ( 1 1 + tan ⁡ 2 θ 0 − tan ⁡ θ 0 1 + tan ⁡ 2 θ 0 ) = 3 − 5 2 1 + ( 3 − 5 2 ) 2 ⋅ 1 − 3 − 5 2 1 + ( 3 − 5 2 ) 2 = … = 3 9 \begin{aligned} & r=\sin {{\theta }_{0}}\cos {{\theta }_{0}}\left( \cos {{\theta }_{0}}-\sin {{\theta }_{0}} \right) \\ & =\dfrac{\tan {{\theta }_{0}}}{\sqrt{1+{{\tan }^{2}}{{\theta }_{0}}}}\cdot \dfrac{1}{\sqrt{1+{{\tan }^{2}}{{\theta }_{0}}}}\left( \dfrac{1}{\sqrt{1+{{\tan }^{2}}{{\theta }_{0}}}}-\dfrac{\tan {{\theta }_{0}}}{\sqrt{1+{{\tan }^{2}}{{\theta }_{0}}}} \right) \\ & =\dfrac{\dfrac{3-\sqrt{5}}{2}}{1+{{\left( \dfrac{3-\sqrt{5}}{2} \right)}^{2}}}\cdot \dfrac{1-\dfrac{3-\sqrt{5}}{2}}{\sqrt{1+{{\left( \dfrac{3-\sqrt{5}}{2} \right)}^{2}}}} \\ & =\ldots \\ & =\dfrac{\sqrt{3}}{9} \\ \end{aligned} For the answer, p = 3 p=3 , q = 9 q=9 , thus, p + q = 12 p+q=\boxed{12} .

3 Helpful 4 Interesting 5 Brilliant 0 Confused

My angle θ \theta was ∠ A B C \angle ABC and my function was r ( θ ) = ( sin 2 θ ( sin θ + cos θ ) ) r(\theta)=(\text{sin}^2\theta(\text{sin}\theta+\text{cos}\theta)) . Then for the first derivative I got r ′ ( θ ) = sin θ 2 ( 3 sin 2 θ + 3 cos 2 θ + 1 ) r'(\theta)=\frac{\text{sin}\theta}{2}\left(3\text{sin}2\theta+3\text{cos}2\theta+1\right) Of course, θ 0 = 0 \theta_0=0 gives a minimal r r so we should set the bracket equal to zero. Using the universal substitution t = tan θ 0 t=\text{tan}\theta_0 the equation simplifies to the quadratic t 2 − 3 t − 2 = 0 t^2-3t-2=0 and gives tan θ 0 = t = 3 ± 17 2 \text{tan}\theta_0=t=\frac{3±\sqrt{17}}{2} Since θ \theta is an acute angle, then all it's trig functions are positive and we'll take the positive t t . This means sin θ 0 = 3 + 17 6 ( 5 + 17 ) \text{sin}\theta_0=\frac{3+\sqrt{17}}{\sqrt{6\left(5+\sqrt{17}\right)}} and cos θ 0 = 2 6 ( 5 + 17 ) \text{cos}\theta_0=\frac{2}{\sqrt{6\left(5+\sqrt{17}\right)}} Finally r max = r ( θ 0 ) , r_{\text{max}}=r(\theta_0), which simplifies to r max = 1 6 71 + 17 17 3 r_{\text{max}}=\frac{1}{6}\sqrt{\frac{71+17\sqrt{17}}{3}}

If someone is willing to take the time to find my mistake, I will be very very grateful. :)

Veselin Dimov - 2 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...