Big Hexagon Small Hexagon - 2
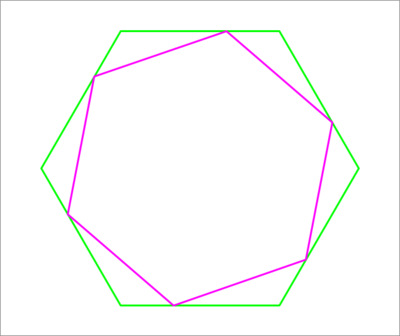
Vertices of the small hexagon (purple) divide the sides of the big hexagon (green) by a ratio of 1 : 2 in the same order.
Find the ratio of the area of the small hexagon to the area of the big hexagon.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Ha, that's a genius idea!
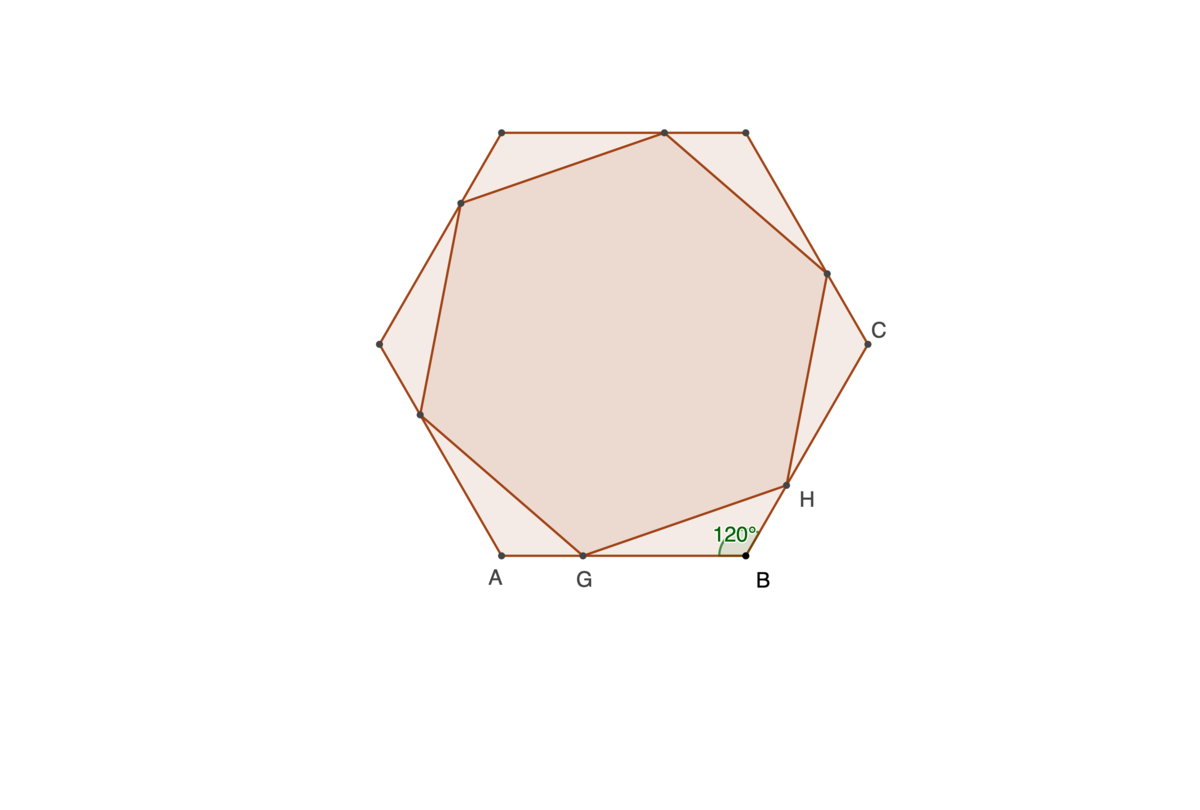
Let A B = 1 , then G B = 3 2 , B H = 3 1
Then by the cosine rule, G H 2 = G B 2 + B H 2 − 2 ⋅ G B ⋅ B H ⋅ cos 1 2 0 ∘
G H 2 = ( 3 2 ) 2 + ( 3 1 ) 2 − 2 ⋅ 3 2 ⋅ 3 1 ⋅ ( − 2 1 ) = 9 7
Since area is proportional to the square if the side, the solution is 9 7 .
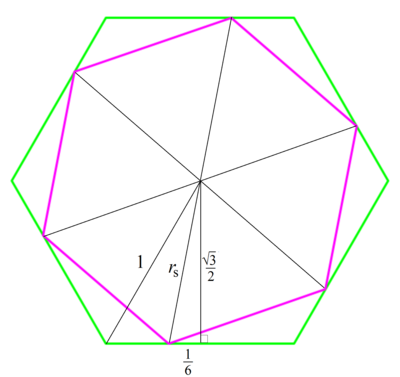
Note that the two hexagons share a center. Let the radius or side length of the big hexagon be 1 . Then the apothem of the big hexagon a B = 2 3 and the radius of the small hexagon is given by r s 2 = ( 2 3 ) 2 + ( 2 1 − 3 1 ) 2 = ( 2 3 ) 2 + ( 6 1 ) 2 = 9 7 . And the ratio of areas A B A s = 1 2 r s 2 = 9 7 .
a p u r p l e = ( 2 3 a g r e e n ) 2 + ( 6 1 a g r e e n ) 2 = 3 7 a g r e e n
S p u r p l e : S g r e e n = a p u r p l e 2 : a g r e e n 2 = 7 : 9
Where do the 2 3 and 6 1 come from ? I did not understand your solution.
Log in to reply
draw lines from center to two adjacent vertexs, then got an equilateral triangle, its attitude is 2 3 a . the distance from vertex inner hexagon to mid of side of outer hexagon is 6 1 a .
Since the ratio values are integers, we can formulate the triangular lattices as shown above. From there, we see that there are 6 × 2 = 1 2 triangles unshaded, whereas there are 4 × 2 6 + 6 + 1 2 × 2 = 4 2 triangles shaded. Thus, the area ratio is 4 2 + 1 2 4 2 = 9 7 .