Big Hexagon Small Hexagon
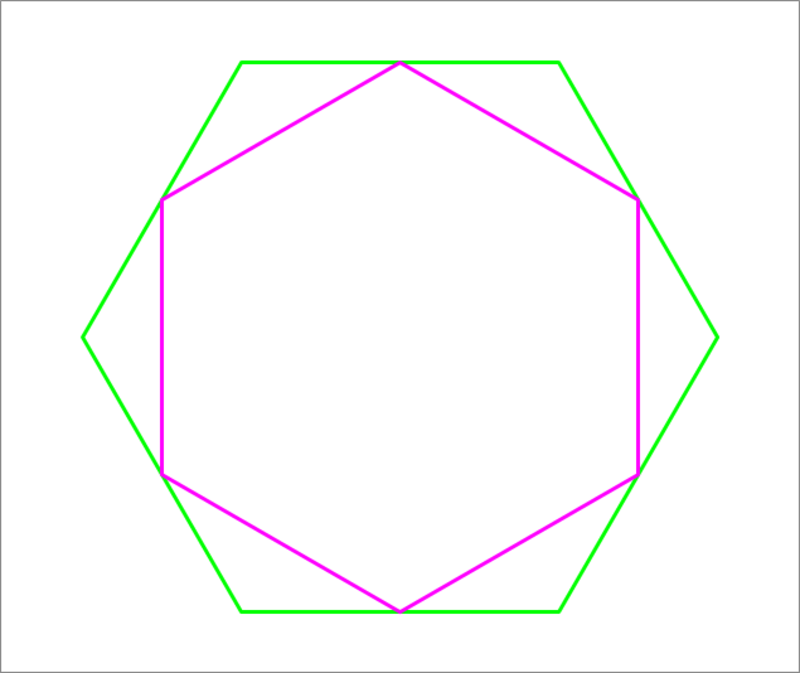
The vertices of the purple hexagon are the midpoints of the sides of the green hexagon. Find the ratio of the area of the small hexagon (purple) to the area of the big hexagon (green).
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
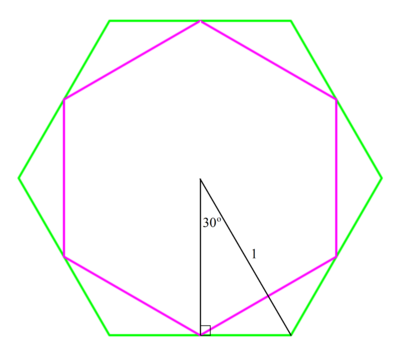
Let the radius of the big hexagon be 1 . Then the radius of the small hexagon r s = cos 3 0 ∘ = 2 3 and the ratio of their areas A B A s = 1 2 r s 2 = ( 2 3 ) 2 = 4 3 .
sin 60 = root3/2 is the ratio of the smaller to bigger side, square it and is the ratio of the area
The area of a regular hexagon is proportional to the square of the length of a side (with a constant of proportionality of 3sqrt(3)/2, which is not relevant). Therefore, the ratio of the areas is the square of the ratio of the lengths of their sides. Without loss of generality, let the length of the side of the big hexagon be 2. Since each vertex of the small hexagon lies on the midpoint of a side of the big hexagon, and each internal angle of a hexagon is 120 degrees, if L is the side length of the small hexagon the Law of Cosines yields:
L^2 = 1^2 +2^2 - 2 (1) (1)*cos(120 degrees), or
L = sqrt(3).
Therefore, the ratio of the areas is:
(sqrt(3)/2)^2 = 3/4
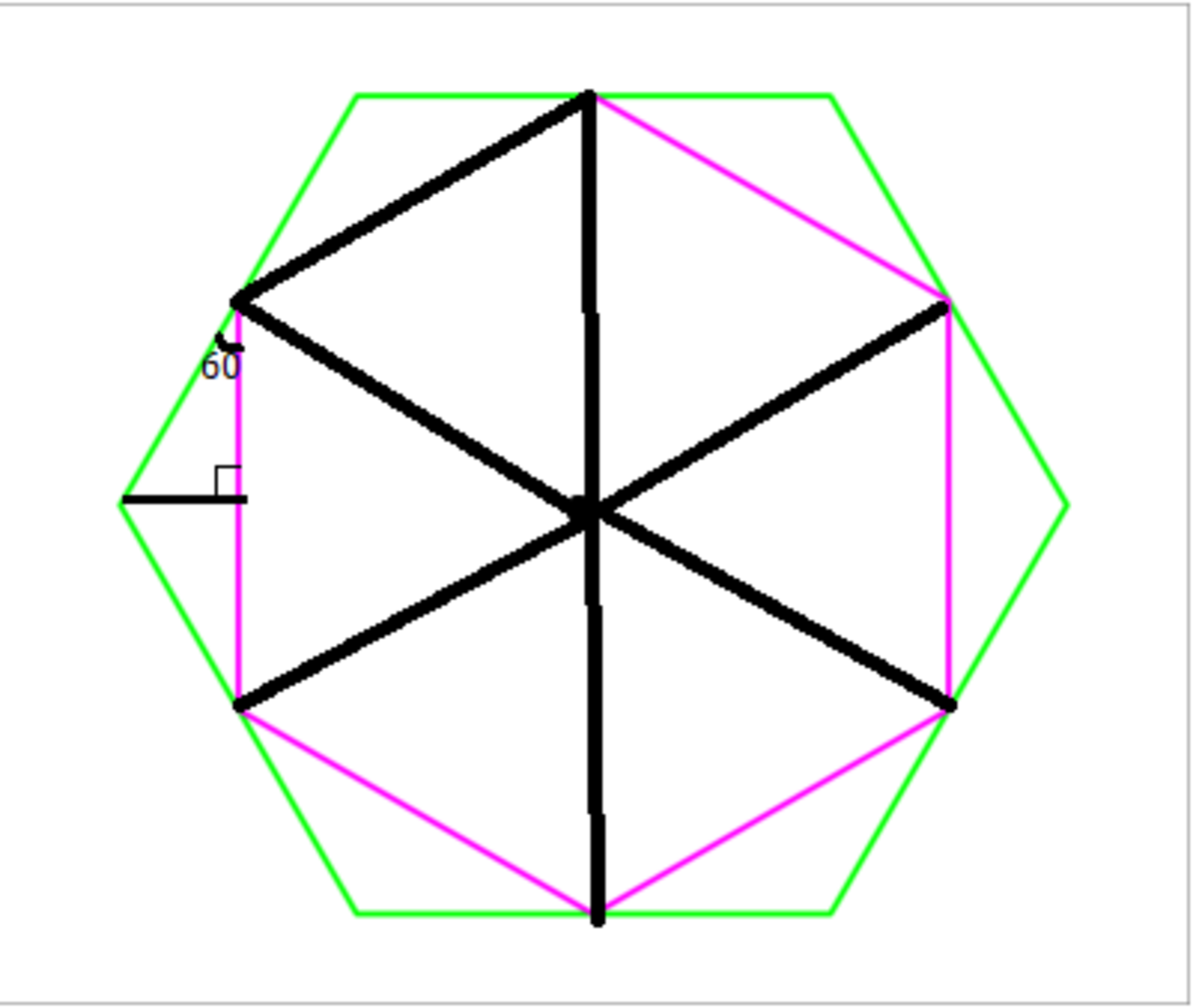
Since, all regular polygons are cyclic and each side subtends an angle of 6 0 ∘ at the center, we have 6 equilateral triangles as shown.
∴ area = 6 ⋅ 4 3 s 2
Also, since 2 S 3 = s ,
ratio of areas = S 2 s 2 = 4 3
The expression for area can be neglected.
As there are 3 × 6 = 1 8 small triangles within the purple hexagon, there are 6 more triangles outside. Therefore, the area ratio is 1 8 + 6 1 8 = 4 3 .