Billiards brain-teaser
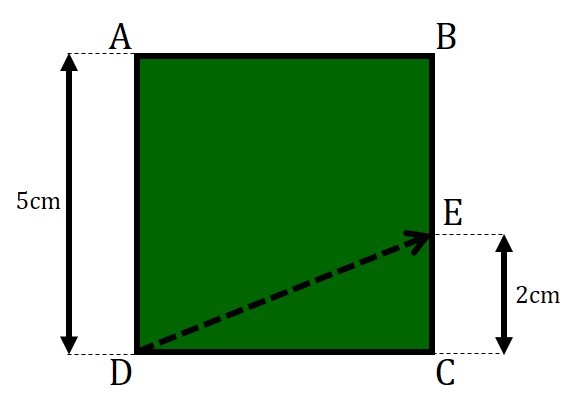 Consider the standard
mouse billiards table shown. The pockets are located at points
and
.
Consider the standard
mouse billiards table shown. The pockets are located at points
and
.
A player has a very poor aim so he hits the ball from point D (his starting point) towards point E. The player hits it hard enough that it eventually lands in one of the pockets (corners). How many times does the ball bounce off the edges of the table before this occurs?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
One way to solve this problem is the "unfolding" technique.
Every time there is a collision with the edge of the table, we introduce a new mirror image of the billiards table. This enables us to plot the ball's path without things getting too messy; a simple diagram yields the result above.
Before being potted at C, the ball clearly hits a boundary (i.e. goes through an edge) 5 times, so the answer is 5 .
For the sake of completeness and clarity, I have also represented this on a single diagram: