Bimetallic strip
A metal strip of length l 0 = 2 0 cm consists of a layer of iron (Fe) and a layer of zinc (Zn), which are welded together with each having a thickness of d = 2 mm . At a temperature of T = 0 ∘ C , the bimetallic strip is completely straight.
What is the radius of the curvature r of the strip at a temperature of T = 1 0 0 ∘ C ?
The respective thermal expansion coefficients of zinc and iron are
α Zn = 3 ⋅ 1 0 − 5 / ∘ C , α Fe = 1 ⋅ 1 0 − 5 / ∘ C .
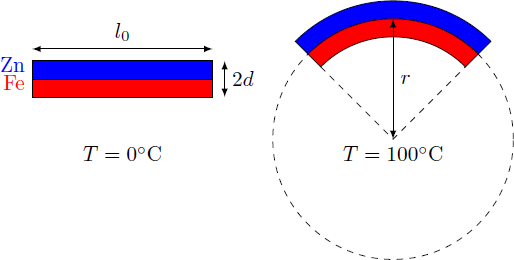
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
By increasing the temperature by the value Δ T , the metals expand, resulting in new lengths of l Zn l Fe = l 0 ( 1 + α Zn Δ T ) = l 0 ( 1 + α Fe Δ T ) where α = l 1 Δ T Δ l is the thermal expansion coefficient.
The metal strips each have the shape of a circular arc with the arc lengths l Zn l Fe = ( r + 2 d ) ϕ = ( r − 2 d ) ϕ with the radius of curvature r of the bimetallic strip and the angle ϕ of the circle segment. Thus, the length ratio yields ⇒ ⇒ ⇒ I Fe l Zn = r − 2 d r + 2 d ( r + 2 d ) ( 1 + α Fe Δ T ) r ( α Fe − α Zn ) Δ T r = 1 + α Fe Δ T 1 + α Zn Δ T = ( r − 2 d ) ( 1 + α Zn Δ T ) = − 2 d ( 2 + ( α Fe + α Zn ) Δ T ) ≈ − d ≈ ( α Zn − α Fe ) Δ T d = 2 ⋅ 1 0 − 5 ⋅ 1 0 2 2 ⋅ 1 0 − 3 m = 1 m
The result also depends on the elastic strength (Young's modulus) of the materials. If one of the materials is very stiff and the other one is very soft then there will no curvature.
Nevertheless, for the materials in this example the answer will be still in the correct order of magnitude.