Binary Chess, Move 5

Probability Level 4

How many invertible symmetric $8\times{8}$ matrices containing exactly 9 ones and 55 zeros exist such that there are exactly 7 zeros on the main diagonal?

Obtained by misreading this

The answer is 840.

1 solution

Otto Bretscher
Sep 10, 2015

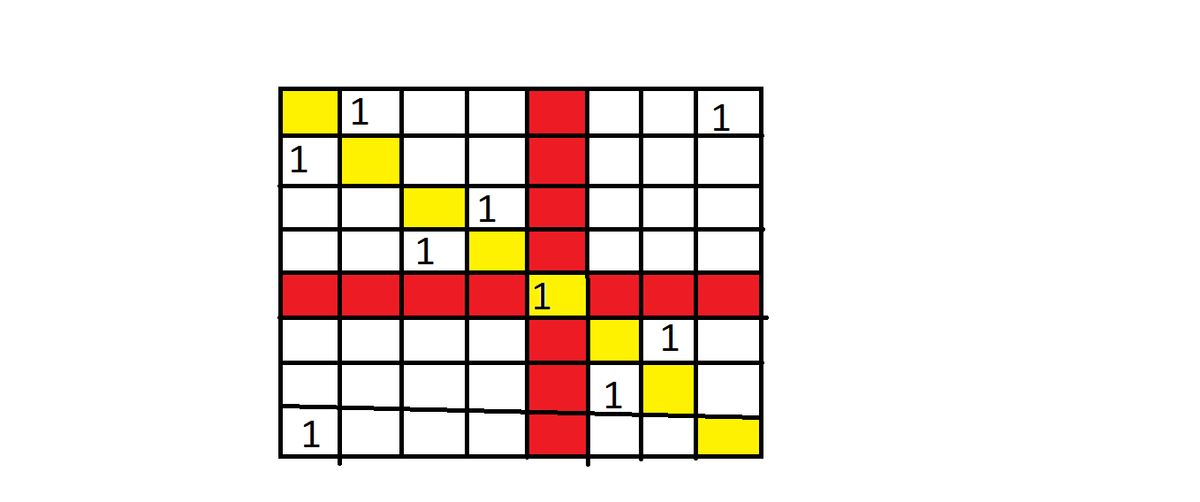
My solution is a bit technical. Maybe there is an easier way.

Since there has to be at least 1 one in each row, we have exactly one row (the $j$ th, say) with 2 ones. By symmetry, there will be 2 ones in the $j$ th column as well. In fact, the $jj$ -entry has to be one; otherwise the matrix would have two equal rows. If we replace this one in the $jj$ th entry by a zero, we have a symmetric permutation matrix without ones on the diagonal.

Let $f(n)$ be the number of symmetric permutation matrices without ones on the diagonal, for even $n$ . Thinking about the position of the one in the first row (and column), we find the recursive formula $f(n)=(n-1)f(n-2)$ , meaning that $f(n)=(n-1)!!$ , the double factorial. Thus $f(8)=7\times{5}\times{3}=105$ .

For each of these symmetric permutation matrices, we can now place the 9th one anywhere on the diagonal, so that we end up with $8\times{105}=\boxed{840}$ such matrices.

Moderator note:

I agree that there are at most 840 such matrices. But you have not justified why all of them are invertible.

In the final step, we can convert the zero in the $jj$ th place into a one by adding another row to the $j$ th row, thus keeping the matrix invertible.

Otto Bretscher - 5 years, 9 months ago

sir i feel that ans is wrong since u missed out many cases "Since there has to be at least 1 one in each row, we have exactly one row (the jth, say) with 2 ones. By symmetry, there will be 2 ones in the jth column as well. In fact, the jj-entry has to be one" this thing is not necessarily true , u may try even for making a matrix kepping in mind this ,

aryan goyat - 4 years, 6 months ago

Binary Chess, Move 5

The answer is 840.

1 solution

Moderator note:

0 pending reports