Binary Tree, Prime Branches
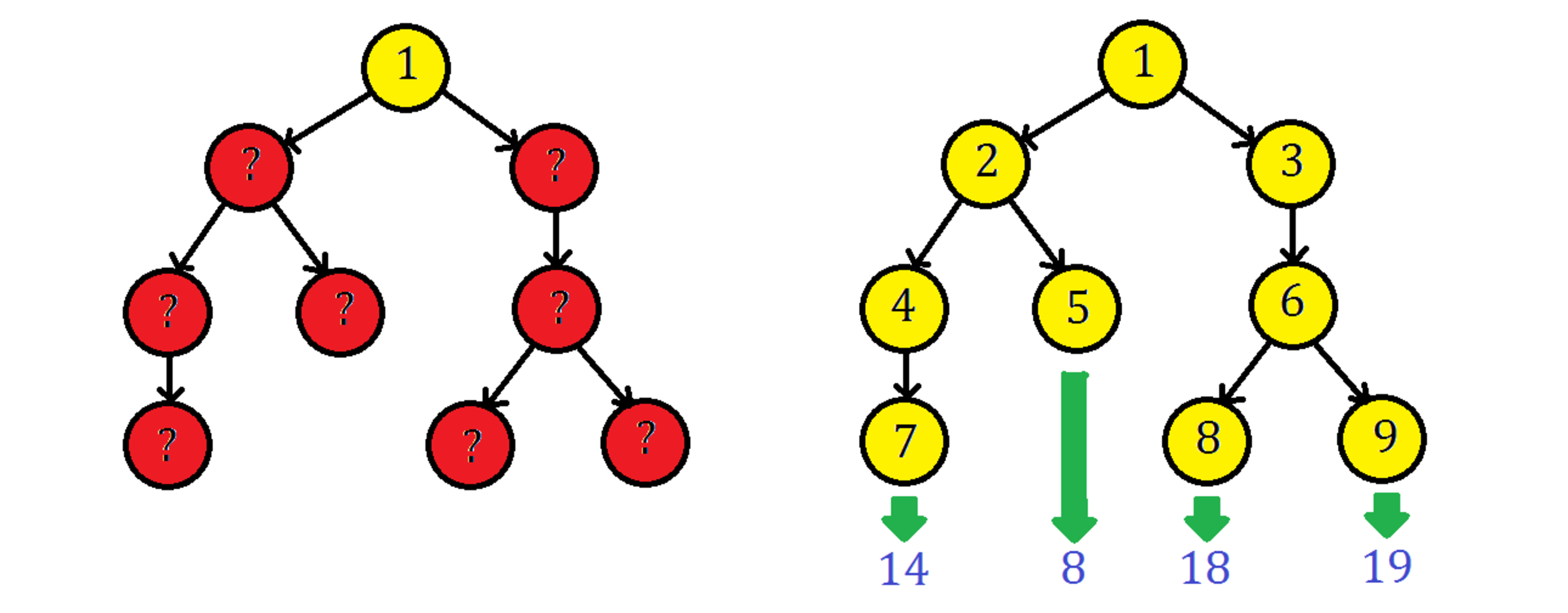
A binary tree has a root of 1 with other nodes containing distinct digits from 2 to 9 inclusive. For example, by adding the digits as shown on the above right, four sums can be obtained by adding the numbers along the descending paths.
Is it possible to put the digits into the left above binary tree to result in four distinct prime sums?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
For simplicity, we will denote the nodes with ordinal numbers as put in the image above right in the question. For instance, the left and right children of the root would be called the 2 n d and 3 r d nodes respectively.
Now since all the sums will definitely exceed 2 , all the prime sums must be odd. Considering the shortest path, if 2 n d node is odd, the 5 t h node must be odd; otherwise, the sum would even. Consequently, that means either 4 t h or 7 t h must be odd so that the sum is odd. In the end, four odd digits will be used, leaving only one odd left on the right wing. However, if the 3 r d or the 6 t h node is odd, all other nodes will be even, and with root node of 1 , the sums will be even. On the other hand, if the 8 t h or the 9 t h is odd, the sum on the other path will be even. Thus, the 2 n d node can't be odd.
Similarly, if 2 n d node is even, the 5 t h node must be even. Thereby, that makes the pair of 4 t h & 7 t h both odd or both even. If the left wing has all even numbers, the right wing will have all odd numbers, yielding only even sums. Thus, we will have the pair of even 2 n d & 5 t h nodes and the pair of odd 4 t h & 7 t h nodes. That leaves two odd and two even numbers to be used. Considering the 8 t h & the 9 t h nodes, they must be either both even or both odd as they have the same mother path. If they are both odd, the sums from root 1 will result in even sums. Hence, we will have the pair of even 8 t h & 9 t h nodes and the pair of odd 3 r d & 6 t h nodes. The image below concludes our proof for Odd and Even digits:
Considering the odd pairs, there are six possible combinations for the left and right wings: {(3+5),(7+9)}, {(3+7),(5+9)}, {(3+9),(7+5)}, {(5+7),(3+9)}, {(5+9),(3+7)}, {(7+9),(3+5)}.
First, let us consider the equal and interchangeable {(3+9),(7+5)} & {(5+7),(3+9)}:
Since 3 + 9 + 1 ≡ 7 + 5 + 1 ≡ 1 ( m o d 3 ) , along all paths, we can not put a digit which equals to 2 ( m o d 3 ) , namely 2 & 8 ; otherwise, the sum will be a multiple of three and not prime. Therefore, 2 & 8 can't be put in the 2 n d , 8 t h , & 9 t h , leaving only the 5 t h node for two numbers, which impossible. Thus, this case is not applicable.
Second, for {(3+7),(5+9)}, 3 + 7 + 1 ≡ 2 ( m o d 3 ) and 5 + 9 + 1 ≡ 0 ( m o d 3 ) . Thus, 4 can't be put in the 2 n d node while 6 can't be put in either 8 t h or 9 t h node. That means 6 is in 2 n d or 5 t h node. However, since 6 + 2 + 1 = 9 and 6 + 8 + 1 = 1 5 , the left wing must have 6 and 4 , and since 4 can't be put in the 2 n d node, 6 is in the 2 n d node and 4 the 5 t h as show below:
However, the sums of 1 7 are repeated, so this case is not applicable.
Third, for {(5+9),(3+7)}, similarly, due to modulus of three, 4 can't be put in either 8 t h or 9 t h node while 6 can't be put in the 2 n d node. If 4 is in 2 n d node, 8 can't be in the 8 t h or 9 t h node because 4 + 5 + 9 + 1 = 8 + 3 + 7 + 1 = 1 9 , making the sums equal, but then if 8 is in the 5 t h node, the 4 + 8 + 1 = 1 + 3 + 7 + 2 = 1 3 , making it also not distinct, which will also yield the same results with 4 in the 5 t h and 8 in the 2 n d node. That leaves us with 2 in the 2 n d and 4 in the 5 t h node, but 1 + 2 + 5 + 9 = 1 + 3 + 7 + 6 = 1 7 , which is also not satisfying. Thus, this case is also not applicable.
Fourth, for {(7+9),(3+5)}, 1 + 7 + 9 ≡ 2 ( m o d 3 ) and 1 + 3 + 5 ≡ 0 ( m o d 3 ) , the 2 n d node can't have 4 , and 6 can't be put in either 8 t h or 9 t h node. That leaves us with one possibility: 6 is in the 2 n d and 4 in the 5 t h node, as shown below.
Again 1 1 is repeated. This is not the solution.
Finally, for {(3+5),(7+9)}, similarly, with modulus of three, the 2 n d node can't have 6 , and 4 can't be put in either 8 t h or 9 t h node. Therefore, 4 will be in either 2 n d or 5 t h node while 6 is in either 8 t h or 9 t h node.
Then if 8 is in 8 t h or 9 t h node, 1 + 7 + 9 + 8 = 2 5 , which is not prime, so 8 is in either 2 n d or 5 t h node. That leaves us with two final scenarios:
Only the right combination works, and this is the only possible method (with 8 permutations among the pairs) to yield four primes of 1 3 , 1 7 , 1 9 , 2 3 . This, thus, concludes our proof.