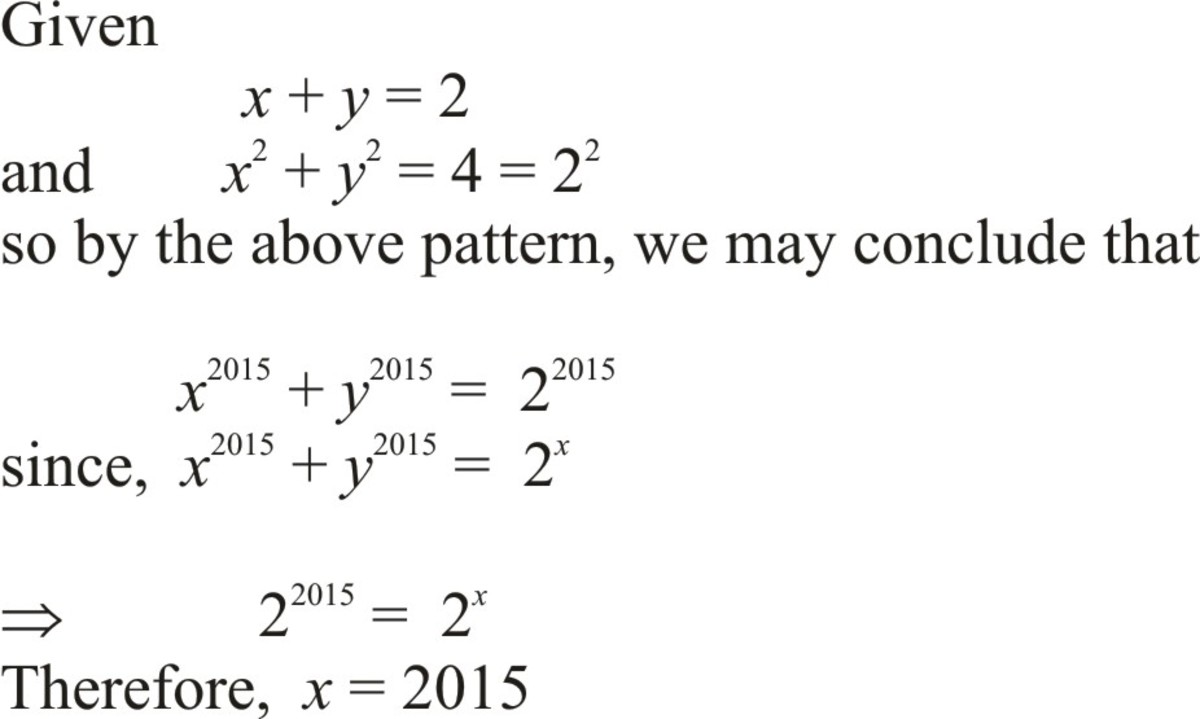Binomial Expansion

Squaring the first equation gives $x^2+y^2+2xy=4=x^2+y^2$ , so $xy=0$ . Thus, $x,y=2,0$ and $x^{2015},y^{2015}=2^{2015},0$ . Thus, $x^{2015}+y^{2015}=\boxed{2^{2015}}$ .

To solve the last equation (X^2015 + Y^2015 = 2^X) look at the first equation ( X + Y = 2) then put X in terms of Y. You will get (X = 2- Y) After this you substitute the value of X so that the last equation is ((2 -Y)^2015 + Y^2015 = 2^X) If you expand the brackets (2^2015 - Y^2015 + Y^2015 = 2^X). You can now cancel the Y as they are were + and -. This leaves us with (2^2015 = 2^X). So X = 2015