Bins in a ring
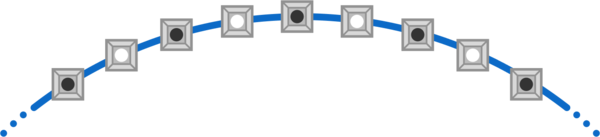
You are playing a game with 2018 bins arranged in a circle. At the start, each bin has a white or black ball inside, with the two colors alternating between adjacent bins all throughout the circle.
The rules are as follows:
- Each turn, you select two balls. Any white ball you select moves clockwise to the next bin. Any black ball you select moves counterclockwise to the next bin.
- You may repeat this process as many times as you like.
- The two balls selected can come from the same bin at later stages when a single bin can have multiple balls.
- You win the game if all 2018 balls are in the same bin after a turn.
Is it possible to win this game?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
At each move, the parity (evenness/oddness) of the number of balls in the 1 0 0 9 bins originally holding the black balls stays the same. The game starts with 1 0 0 9 balls in these bins, and to win there would have to be an even number (either 0 or 2 0 1 8 ) of balls in these bins. It is not possible to win.
say there are three bins: w1 b1 w2
there's an odd number of black balls, but the game is winnable: just move w2 to w1, b1 to w1.
edit: nvm, i just realized w1 is next to w2, which is not allowed by the original problem. still, i think it's worth considering what happens for, say, 4k+1 bins or 4k+3 bins with just two same colour neighbours.
Log in to reply
It is trivially easy to win the game with 4 n bins, and impossible to set up alternating ball colours with an odd number of bins.
Log in to reply
I busted myself by testing out with 8 bins and concluded I could make it :-P I should have tried with 6 instead...
Number all the boxes in sequence, starting with 1 on a white ball, and ending with 2 0 1 8 on a black ball.
For all balls to be in the same box, either all the black balls must be moved to an odd box, or white to an even one.
As there are 1 0 0 9 balls of each colour, it's impossible to move all black balls into odd boxes without also moving a white ball to an even one, or vice versa (as exactly 2 balls must be moved).
Therefore it cannot be done.
Am I the only one who can't understand the statement.
I don't think it's clear what "selecting" a ball does
I've clarified the first bullet point.
the bins can contain as many balls as you like, and they go in a loop.
initially they each hold one ball, and each bin has only different colored neighbours.
then a game starts and you can move the balls around, but it goes by turns and there are some rules:
-
each turn you have to move exactly two balls
-
any ball you move has to go to a bin next to it. (if each bin has a right and a left neighbour, white balls go to the right neighbour and black balls to the left neighbour.)
you win the game if at the end of a turn you have all the balls in just one bin.
the question is if you can win the game.
if this is clear, what wasn't in the original post? if it isn't, what's not clear?
Can only be won if the number of bins is a multiple of 4. Try starting with 2,4,6,8 bins etc
At each move, the parity (evenness/oddness) of the number of balls in the 1009 bins originally holding the black balls stays the same. The game starts with 1009 balls in these bins, and to win there would have to be an even number (either 0 or 2018 ) of balls in these bins. It is not possible to win.
It was more if guesswork, but if the balls are moving ing to o separate directions, it should be possible to bring all the whites to one box and all the blacks to the other, but because of the parity of 2018 you can never bring these together.
Yes, good point Brian.
If one can see that the solution stays the same whenever there a equal odd number of both balls, then we can take the case where there is 1 of each ball. We find that it is impossible to win in this case.
Label bins starting with white balls 0 and bins starting with black balls 1. After each move, calculate this sum across all labels: (label of the bin * number of balls in that bin). This sum starts with 1009 (an odd number), and its evenness/oddness should not change with each move. To have all 2018 balls on the same bin, this sum will need to either become 2018 or 0 (an even number), which is impossible.
Let a "step" be the process of moving one ball into the next bin. Then for any bin that you pick to try to place all the bins in, 1 0 0 9 balls must move an even number of steps and 1 0 0 9 balls must move an odd number of steps. (For example, if you pick a bin that originally had a white ball, then all the white balls must move an even number of steps clockwise and all the black balls must move an odd number of steps counterclockwise. Similarly, if you pick a bin that originally had a black ball, then all the black balls must move an even number of steps counterclockwise and all the white balls must move an odd number of steps clockwise.) Since 1 0 0 9 ⋅ even + 1 0 0 9 ⋅ odd = odd , an odd number of total steps is required to win the game.
However, since each turn requires selecting 2 balls and moving them, the total number of steps will be even. Therefore, it is not possible to win this game.