Birds in queue
There are 10 birds sitting on a wire in queue. A hunter has 3 bullets in his rifle. Each time he shoots a bird, the adjacent bird(s) next to it flies away.
In how many orders the hunter can shoot three birds?
Details and Assumptions:
-
The hunter shoots exactly 3 times.
-
You can assume that he doesn't miss.
-
Shooting orders means the pattern he is shooting three birds. For example, counting from the left he can shoot the 5th bird first, then 1st bird & then maybe 10th bird. That's one of the orders.
The answer is 336.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
The hunter can't shoot 2 adjacent birds. So, let's find the total number of combinations he can pick 3 birds where neither of them are adjacent. For easier understanding here is a scenario:
Think of 10 balls, where 7 of them are black & 3 are white. We have to place them in a queue such that none of the white balls are adjacent. There are 6 positions between the 7 black balls where we can place them & 2 position beside the 7 black balls where we can place them too. So the number of combinations will be: 8 C 3 or, ( 3 8 ) = 5 6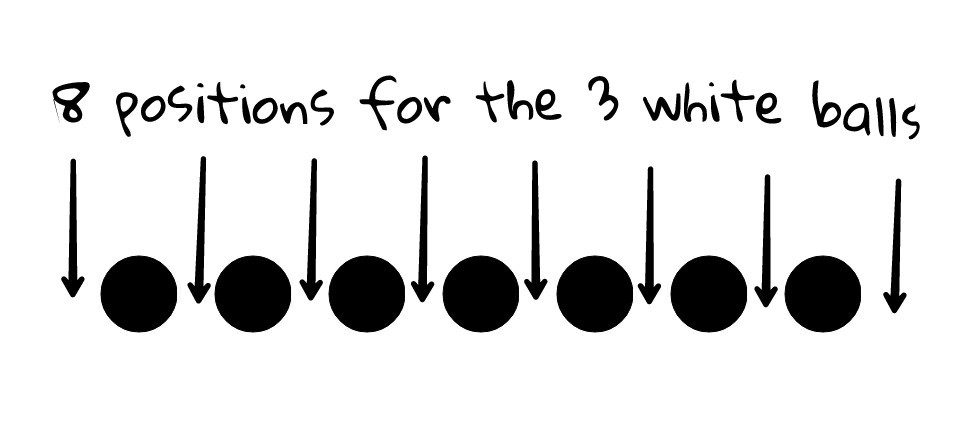
This is same as picking 3 birds out of 10 where none of them are adjacent. But the hunter can shoot the same 3 birds in different orders.
So, the answer will be, 5 6 × 3 ! = 3 3 6