Birthday Girl
 Albert and Bernard just became friends with Cheryl, and they want to know when her birthday is. Cheryl gives them a list of 10 possible dates:
Albert and Bernard just became friends with Cheryl, and they want to know when her birthday is. Cheryl gives them a list of 10 possible dates:
| May 15 | May 16 | May 19 |
| June 17 | June 18 | |
| July 14 | July 16 | |
| August 14 | August 15 | August 17 |
Cheryl then tells Albert and Bernard separately the month and the day of her birthday respectively.
Albert: I don't know when Cheryl's birthday is, but I know that Bernard does not know too.
Bernard: At first I don't know when Cheryl's birthday is, but I know now.
Albert: Then I also know when Cheryl's birthday is.
So, when is Cheryl's birthday?
Image credit: Wikipedia Tatiana Sapateiro
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
Moderator note:
The image that you created made it really easy to follow and understand the logic argument that you were providing. Thanks!
First we need to figure out if Albert knows the month or the day. If he knows the day, then there is no chance that Bernard knows the birthday, so it must be that Albert knows the month.
From the first statement, we know that Albert is sure that Bernard doesn't know the birthday, so May and June should be ruled out (the day 19 only appears in May and the day 18 only appears in June). In other words, if Albert had May or June, then he cannot be sure that Bernard doesn't know, since Bernard could have had 18 or 19.
Following that statement, Bernard knows that May and June are ruled out.
Then, Bernard is able to know which month it is. So it must be either July 16, August 15 and August 17 (not 14th as then he can't know).
Since Albert subsequently can also be sure of the date, he must know it's July. If it's August, he can't be sure as there is August 15 and 17.
So the answer is July 16.
http://mashable.com/2015/04/13/math-is-hard/#LLRfdmkr1Oq6
Thought this solution is great.
However, there are two days left in may, so you cant rule out may as a possibility. In that case, it is impossible to give any answer
I get it. I agree that it is not an 18 or a 19 but, I believe that it only implies that it is not May 19 or June 18. I don't see the logic behind removing May and June altogether. Please explain
Log in to reply
Albert knows the month.... Had it been May or June (which include unique dates 18 and 19), he would not have been completely sure that Bernard (who knows the date) doesn't know the birth day....
Add the days up then Divide by ten and do the same with the months in # form Answer then ends up being July 16th
Let A = Albert and B = Bernard. Also, taking May 15 as an example, May 15 is the date , May is the month and 15 is the day .
Albert: I don't know when Cheryl's birthday is, but I know that Bernard does not know too.
This statement implies that A with 100% certainty knows that B does not know the date. So we get two bits of information, B does not know the date, and A knows that B does not know the date.
When does B not know the date? If he knows the day is 18 or 19, he can easily figure out the date. For 14/15/16/17, there are two possible choices so he can't know the date. Since B does not know the date, we can eliminate May 19 and June 18.
Now, how is A 100% sure that B doesn't know the date? We showed that if the date was May 19 and June 18, then B will know the date. So if the month known to A was May or June, than A could not say with 100% certainty that B does not know the date. So the only dates left are the ones in July and August.
Bernard: At first I don't know when Cheryl's birthday is, but I know now.
Using the same reasoning we did, B now knows that the month is July or August. If the day he knew was 14, then he would still be stuck with July 14/August 14. So 14 is not possible. So the three choices left are July 16, August 15, August 17.
Albert: Then I also know when Cheryl's birthday is.
Using the same reasoning we did, A knows that there are only 3 dates left. If the month know to A was August, then he couldn't have figured out the date, since there are two possible choices, August 15/August 17. So the month A knows is July, giving the only possible date of July 1 6
By elimination method, "Does not know" represents eliminating UNIQUE number/month. "I know" represents eliminating DUPLICATE number/month. Take note that Albert has all the months and Bernard has the date/number. In the first statement both of them do not know the date. 18 and 19 are unique number so eliminate this. Consequently eliminate the months of May and June. Second statement, Bernard knows it so eliminate duplicate numbers which are july 14 and august 14. Finally, Albert knows it also so eliminate august 15 and august 17. Therefore, the only date left is JULY 16. Hope this makes sense. ",
Hey, did you know that I watched a video with the same question and solution???😃😃😃😃😃😃😃😃😃😃😃😃
I saw this solution elsewhere, and thought it was great. Source
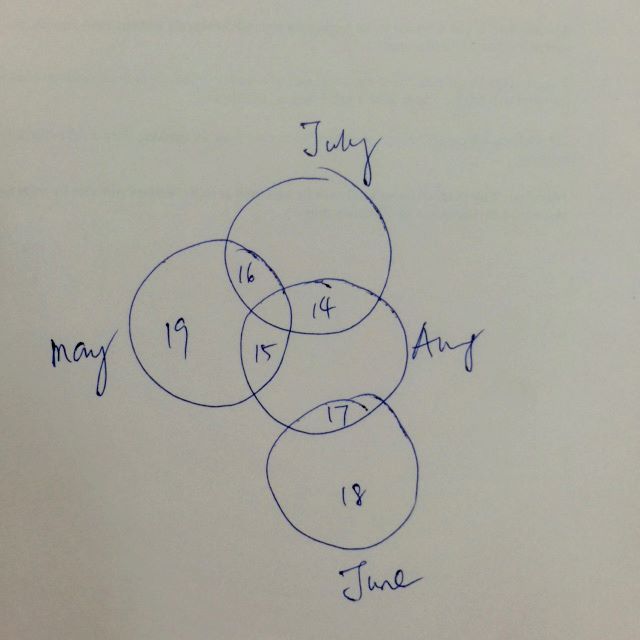
When Albert says he knows that Bernard doesn't know, it means that the dates are not unique. Since there's only 18 and 19 in May and June, the birthday has to be either in July or August.
Since Bernard claims that he now knows, and looking at the dates in July and August (14, 15, 16, 17), only 15, 16 and 17 are not unique.
Since Albert knows the month, it can't be August as there are 2 dates left in that month. The only logical month left is July, so it has to be July 16.
Here's the official solution from the Asian Schools Math Olympiad (SASMO) 2015 Contests Q24
Here's a github for the explanation
Basically the synopsis of all the proofs I've seen boils down to these steps:
-
Eliminate all dates that have a unique day.
-
Eliminate all dates that have a unique month.
-
Eliminate all dates that do not have a unique day.
You may visit the Twitter Page too for some amusing tweets like these:
-
Hope Cheryl never approaches police questioning in the same way. She'd be shot.
-
Cheryl clearly doesn't want any presents.
-
Imagine Cheryl ordering a pizza. Calls 2 separate places, tells one the address and the other the toppings. Goes hungry.
-
I don't really care about Cheryl's birthday because she thought the dress was white and gold.
-
"This is not a math problem; it's a communication problem!" HAHAHA
-
If Cheryl makes it this hard to find out when her birthday is, she's NOT going to get many gifts
-
Just add Cheryl on Facebook and you'll be notified when her birthday comes along.
-
I suggest that Albert and Bernard find a new friend who is not Cheryl.
-
Albert and Bernard later went out and over drinks, compared notes and decided Cheryl and her frigging birthday wasn't worth their time.
News that made this viral:
Here's an alternative answer for Cheryl's birthday: August 17.
It all depends on your point of view.
A simple logic problem, which the Singapore maths students couldn't solve.
Since in the beginning, Albert knows for sure that Bernard does not know the answer, hence the Birthday must have been in the month of July or August. It is so because Albert knows the month and if the month were either May or June, he could not have said that Bernard does not know the birthday because May- 1 9 and June- 1 8 are unique dates.
Based on above analysis, once Bernard knows that the month of birthday is either July or August, he knows the birthday. Hence, the date cannot be 1 4 . This is so because if the date were 14, Bernard could not have concluded the birthday.
Now, based on above analysis, Albert also deduces the birthday. Hence, the birthday should have been July- 1 6 because if it were either August- 1 5 or August- 1 7 , he could not have deduced the birthday.
Thanks for understanding. I posted it a few short hours just before you did. This is a problem that recently got popular from being posted in the Singapore newspaper, which was then picked up by the Guardian.
Note that this is actually a "Secondary 3/4" (Grade 9/10) math olympiad problem, instead of a "Primary school" (Grade 4-6) problem. Given that setting, it is not too surprising of a problem.
Log in to reply
I agree that its Grade 9/10 problem. And, it got popular because it was asked in Primary School Exam as per the Singapore newspaper article...
For sure, this problem puzzles one's thinking for quite some time. And the most common mistake we make is unknowingly putting the reasoning around the premise:
"Albert knows that Bernard does not know the answer and hence the date can not be 1 8 and 1 9 ".
This is subtly different from the actual reasoning which is "Albert knows the month and he can say that Bernard does not know the answer iff the month is not May or June.
Singapore news article:
I believe that the source of this problem is not the 2015 SASMO, but instead came from a primary 6 preliminary school exam paper produced back in 2006... Remembered doing this problem many years ago...
Edit: The 2006 P6 problem can be found here: http://gangasudhan.blogspot.sg/2013/02/the-birthday-mystery-reportedly-p6.html
Given: Albert was given a month (May, June, July, Aug) Bernard was given a day (14, 15, 16, 17, 18, 19)
Required: When is Cheryl's Birthday?
Solution: 1.) Albert said "I don't know when Cheryl's birthday is, but I know that Bernard does not know too" Since Albert knows only the Month and each month has more than one possible day, Albert really does not know. The only way that Bernard could know the exact birthday is when Bernard was given the day of 18/19, since these days are the only ones that does not repeat. For Albert to be certain that Bernard does not know what the date is, Albert must have been given a month of either July or August. This cancels out the all May and June dates.
2.) Bernard said "At first I don't know when Cheryl's birthday is, but I know now." This implies that Bernard was able to deduce that Albert has a month of July/August. The fact that he said "but I know know" means that the day that was told to him (either 14,15,16,17) is partnered with only one month. Therefore all dates with a day of 14 is cancelled, since there are two dates with 14 as the day.
3.) Albert said "Then I also know when Cheryl's birthday is" At this point, in order for Albert to say that he knows, he based on Bernard's statement that Bernard already knows. Since Bernard said he already figured the birthdate, Albert was able to deduce that the possible dates left are July 16, Aug 15 and Aug 17. For Albert to deliberatively say he has figured out when the birthday is, he should have been told of "July" as the month of the birthday, otherwise, he will be left unsure between Aug 15 and Aug 17.
Answer: July 16
Each new piece of information allows us to restrict our attention to a submatrix.
The second clue states that Bernard doesn't know at first, that means it can't be 18 or 19, being the unique numbers of the set. Albert also doesn't know at first, and he says that he knows that Bernard doesn't know. Meaning the months related to 18 and 19, which are June and May, are already crossed out. Leaving us with the dates on July and August. Since Bernard immediately knows at the second clue, Cheryl would have had told him that the date is 16 because Albert immediately knew as well after knowing that Bernard knows. Let's say Bernard was told of 14, that means he wouldn't have deduced immediately that July is the month. So July 16.
SASMO 2015
Log in to reply
I believe that the source of this problem is not the 2015 SASMO, but instead came from a primary 6 preliminary school exam paper produced back in 2006...
- Let’s re-state the facts here. Albert knows the MONTH of Cheryl’s birthday and Bernard knows the DAY. They don’t know the other piece of information, but they both share one common knowledge: the 10 possible dates given by Cheryl.
- In hint 1, Albert says that he knows that Bernard does not know Cheryl’s birthday after knowing the day from Cheryl. Notice that IF Cheryl’s birthday is 18 June or 19 May, then Bernard would have immediately know the entire birthday just by knowing the day. This is obviously not the case because Albert is sure that Bernard does not know. So we can safely remove 18 June and 19 May from the possibilities.
- Now, how does Albert knows that Bernard was not told “18” or “19”? Simple. Because Albert knows the month from Cheryl and it’s not May or June. So we can conclude that Cheryl’s birthday month is either July or August. So far we have removed 15 May, 16 May, 19 May, 17 June and 18 June just by using the first hint from Albert.
-
Next, we use the second hint. Bernard says that he previously didn’t know Cheryl’s birthday, but after hearing Albert’s hint, now he knows exactly when Cheryl’s birthday is. Since Albert’s first hint helped us to removed all possible dates from May and June, it also helps Bernard. If the day given to Bernard is 14, Bernard would still have question whether Cheryl’s birthday is 14 July or 14 August. But Bernard doesn’t have this question. He knows Cheryl’s birthday after he realises that the month that Albert knows is either July or August, we can safely remove 14 July and 14 August from the possible dates.
- At this point, we know that Bernard already knows the exact date, but we are still wondering whether it is 16 July, 15 August or 17 August. Bernard knows the date so he quickly knows. We don’t. So how do we know? We use the third hint. After hearing that Bernard now knows the date, Albert also says that he knows the date. If the month that Albert knows is August, he would not say that because he would be wondering between 15 August and 17 August. But Albert knows Cheryl’s birthday. This is only possible if the date that Cheryl told Albert was July. 6. We already removed 14 July from the list. So the only date left is 16 July. Cheryl’s birthday is 16 July. The deduction A above should be clear enough to follow. But in case you are still confused, let me present deduction B with complete set of possibilities.
A (Albert) knows the month and B (Bernard) knows the date. From the first reply of A, we know for sure that the month will be the one such that all possible dates in it occur in at least another month. Otherwise if the date happens to be unique one that is present only in that month then B would have figured the month out. Hence we can eliminate May and June (19 th and 18th are unique days respectively) and the month must be either July or August.
Now think of B. Since B has figured out the month after hearing the first comment from Albert, it must be that the day occurs either in July OR August (not both) and also occurs either in May or June (so that, B could not figure it out before). Hence the date must be either 15, 16 or 17. Now since A figures out the date after hearing B's answer, it must be that the date is occurring exactly once in the month (July or August). Hence the date must be 16 (as both 15 and 17 occurs in August) and the month must be July.
A knows that B does not know, because the month does not coincide with the two days, 18 and 19, that only occur once and in different months, when B would have only one choice of month, and already know the birthday. That means the month in not May or June.
When B says he knows the birthday, that cuts out 14 that occurs in both the two remaining choices of month, when B would still have no way to chose a month.
When A then says he knows as well. That means the month he knows only has one choice of day.
The month must be July and the birthday is July 16, because otherwise A would have no way to pick between August 15 and August 17.

We proceed counterclockwise:
Since Bernard knows the date, Albert can only be sure that Bernard doesn't know the birthday if it is in July or August. The reasons is that May and June both have days (19 and 18, respectively) for which they are the only month with that date. Therefore, Albert has implied that the birthday is in July or August.
If Bernard can now guess the birthday, it means that the birthday is not on the 14th. If it were, he'd be unable to choose between July and August, which both have that date. Thus, only July 16, August 15, and August 17 remain.
Now, Albert knows the month, and if he can guess the birthday, it's because Bernard has eliminated his only alternative, the 14th. If the 14th is his only alternative, the birthday must be the remaining choice in July, July 16th.