Birthday paradox, with a twist!
Imagine 5000 people in a birthday party. What is the probability that all of them have the same birthday?
A.
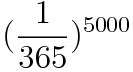
B.
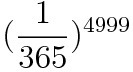
C.
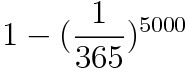
D.
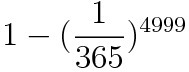
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
A common mistake is that each person should have a prob. of 3 6 5 1 to have their birthday on a specific date. That means 5 0 0 0 people should have that prob. to the power of 5 0 0 0 ! That is wrong though!
The correct answer is B. Think of it as this:
What is the probability that 3 people have their birthday on the same date in 1 week ? (Mon - Sun)
The answer of it would be 4 9 1 as for 2 people, the prob. is 7 1 , or 4 9 7 and 3 people are just 7 3 7 , or 4 9 1 !