Birthday Problem!
n = 1 ∑ ∞ 4 n 6 n = ?
Give your answer to 2 decimal places.
The answer is 2.67.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Same way........Thumbs up!!!
How do you get from S/4 to 3S/4?
Log in to reply
S − 4 S = 4 3 S
I made this formula for k>1 n = 1 ∑ ∞ k n n = ( k − 1 ) 2 k , then 6 n = 1 ∑ ∞ 4 n n = 6 3 2 4 = 3 8 = 2 . 6
I made other for this n = 1 ∑ ∞ k p n p but its a recursive formula, I couldn't made a pretty formula like above.
Note that 1 − x 1 = 1 + x + x 2 + x 3 + … + x n + … , where ∣ x ∣ < 1 Differentiate it and multiple both sides with x , we obtain ( 1 − x ) 2 x = x + 2 x 2 + 3 x 3 + … + n x n + … , where ∣ x ∣ < 1
Note that n = 1 ∑ ∞ 4 n 6 n = 6 ( x + 2 x 2 + 3 x 3 + … + n x n + … , ) where x = 4 1
Hence, n = 1 ∑ ∞ 4 n 6 n = 6 × ( 1 − 4 1 ) 2 4 1 = 3 8
The sum is equal to 6 ⋅ ( 4 1 1 + 4 2 1 + 4 3 1 + 4 4 1 + 4 5 1 + ⋯ + 4 2 1 + 4 3 1 + 4 4 1 + 4 5 1 + 4 6 1 + ⋯ + 4 3 1 + 4 4 1 + 4 5 1 + 4 6 1 + 4 7 1 + ⋯ + ⋯ ) = 2 4 ⋅ { 4 1 1 ⋅ ( 4 1 1 + 4 2 1 + 4 3 1 + 4 4 1 + 4 5 1 + ⋯ ) + 4 2 1 ⋅ ( 4 1 1 + 4 2 1 + 4 3 1 + 4 4 1 + 4 5 1 + ⋯ ) + 4 3 1 ⋅ ( 4 1 1 + 4 2 1 + 4 3 1 + 4 4 1 + 4 5 1 + ⋯ ) + ⋯ } = 2 4 ⋅ ( 4 1 1 + 4 2 1 + 4 3 1 + 4 4 1 + ⋯ ) ⋅ ( 4 1 1 + 4 2 1 + 4 3 1 + 4 4 1 + ⋯ ) = 2 4 ⋅ ( n = 1 ∑ ∞ ( 4 1 ) n ) 2 = 2 4 ⋅ ( 3 1 ) 2 = 3 8 ≈ 2 . 6 7 .
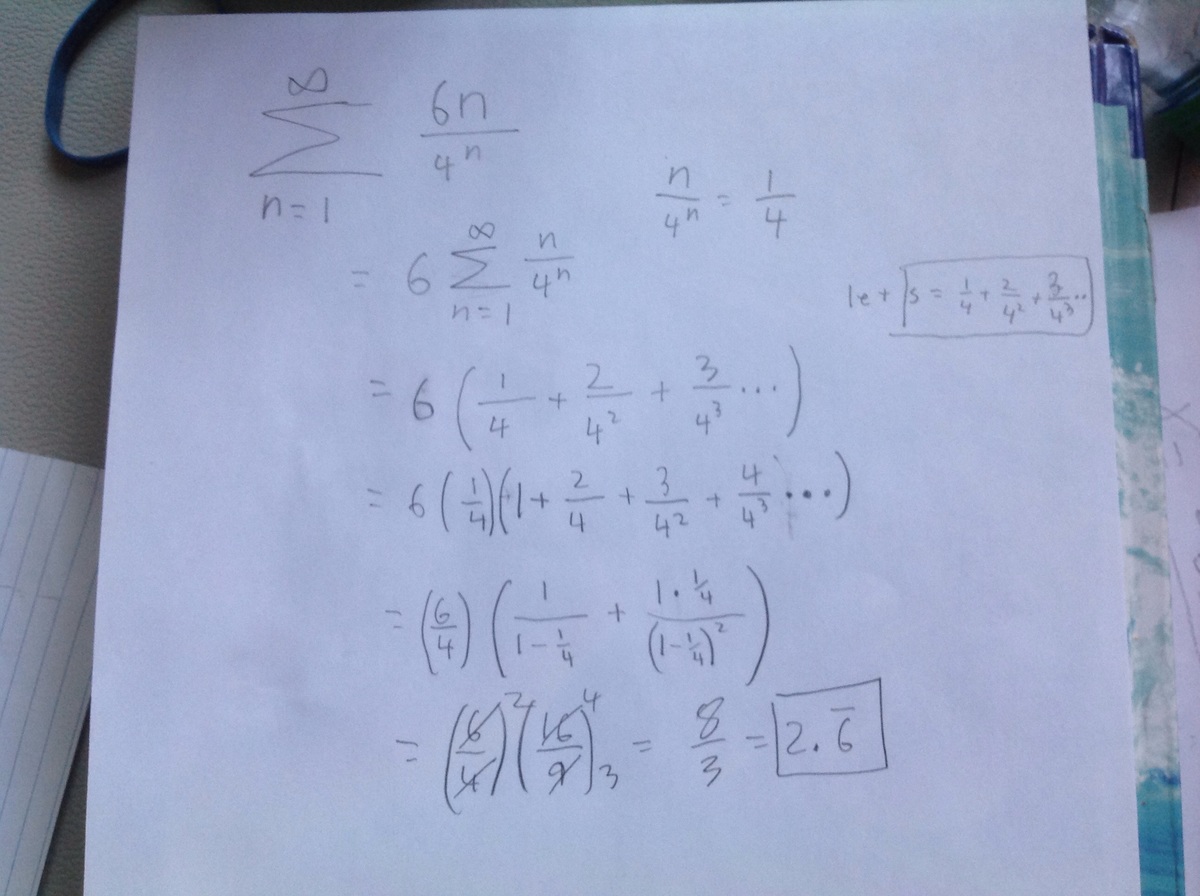
n = 1 ∑ ∞ 4 n 6 n = 6 n = 1 ∑ ∞ 4 n n 6 ( 4 1 + 4 2 2 + 4 3 3 + 4 4 4 + … ) Let S = 4 1 + 4 2 2 + 4 3 3 + 4 4 4 + … 4 S = 4 2 1 + 4 3 2 + 4 4 3 + 4 5 4 + … S − 4 S = 4 1 + 4 2 1 + 4 3 1 + 4 4 1 4 3 S = 1 − 4 1 4 1 = 3 1 S = 3 4 × 3 1 = 9 4 ∴ 6 S = 3 8 = 2 . 6 6