Bisecting a Parallelogram

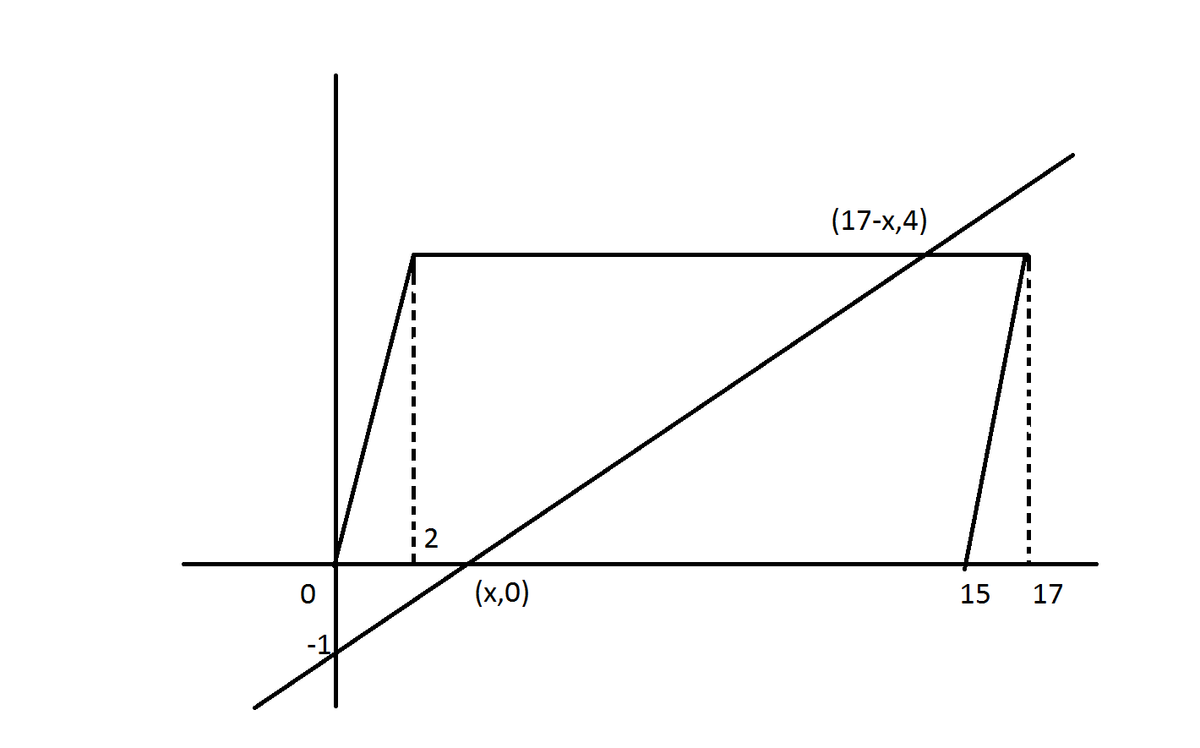
As we increase the slope of the line through our point $(0,-1)$ , the area inside the parallelogram below our line increases. There will be a unique slope for which the area below the line is exactly half of the area in the parallelogram. When our line passes through the point of intersection of the diagonals of the parallelogram, our line will bisect the area of the parallelogram because it will divide the parallelogram into two congruent trapeziums.

The intersection of the diagonals is the point $\left( \frac{17}{2}, 2 \right)$ , so the slope of our bisecting line must be $\frac{2 - (-1)}{ \frac{17}{2} - 0 } = \frac{6}{17}.$ Therefore, $a+b=6+17=23.$

As we see from the image for equal area and due to symmetry , the line cuts the the x axis at (x,0) and the upper part of the parallelogram at (17-x,4) . [This makes the two trapeziums congruent to each other]

We also know the general equation of a line Y=mX+c . In this question , we just need to find the value of m which is the slope of the line. As the line passes through above two points i.e., (x,0) and (17-x,4) , these points satisfy the equation. Substituting the value of (x,0) in the equation , we get

0= m(x) + c , so c=-mx .

Also the line passes through the point (0,-1) [Given in the question] . So,

-1 = m(0) + c . Hence c=-1 and mx=1 .

Now, using the third point (17-x,4) , we get

4=m(17-x) + c

4=17m - mx -1

4=17m - 2 [mx=1]

So, $m=\frac { 6 }{ 17 }$