Bisecting Triangle
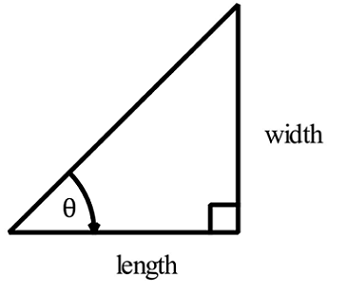
I have drawn a right angle triangle such that the two shorter sides are equal. If I split the angle into two (bisecting the angle), then what is the ratio of the length and the width?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the length be l and width be w of the given right angled triangle.
Case 1 : When the length l and width w are equal then ratio is found to be 1 : 1 reference angle θ is 4 5 ∘ as l = w or, t a n θ = l w So θ = 4 5 ∘
Case 2 : When the reference angle (\theta) is bisected into two equal angles then it( θ is splited into 2 2 . 5 ∘ each.
So t a n 2 2 . 5 ∘ = c o s 2 2 . 5 ∘ s i n 2 2 . 5 ∘
We have : 2 s i n 2 θ ∘ = 1 − c o s θ
2 c o s 2 θ ∘ = 1 + c o s θ
t a n 2 2 . 5 ∘ = 1 + c o s 4 5 ∘ 1 − c o s 4 5 ∘
On evaluting we get
t a n 2 2 . 5 ∘ = 2 + 2 2 − 2 = 2 − 1
Therefore, ratio of length and breadth w ′ (new obtained width after bisecting the θ is
w ′ l = t a n 2 2 . 5 ∘ 1
w ′ l = 1 : ( 2 − 1 )
Alternatively :
Let bisected angles be A and B . Then
t a n ( A + B ) = t a n θ
t a n ( B + B ) = 1
1 − t a n 2 B 2 t a n B = 1
2 t a n B = 1 − t a n 2 B
t a n 2 B + 2 t a n B − 1 = 0
Solving for B by using quadratic formula
B = 2 − 2 ± 4 − 4 ( − 1 )
B = 2 2 ( 1 ± 2 )
B = − 1 ± 2
Since B is an acute angle so B = 2 − 1
so required ratio is found be l : w ′ = 1 : ( 2 − 1 )