Bishop attack!

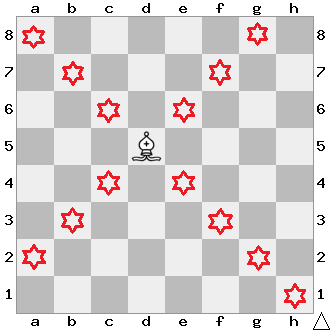
Here is the solution: 14 bishops.

---

We have shown that 14 is possible. Now we have to show that 14 is the only solution.

We will place bishops only in center. Here is the diagram:

Which is only 8 bishops.

Now, we will place bishops on corner, upside and downside. Here is the diagram:

Which is only 11 bishops

Now, we will place bishops on center, upside and downside. Here is the diagram:

Which is only 12 bishops.

Now, we have a strong choice to place the bishops only in upside and downside. Here is the diagram:

Which is again 14 bishops. Hence we can say that 14 is maximum.

Each bishop covers exactly two diagonals that are of the same color. Since there are 7 pairs of white diagonals and 7 pairs of black diagonals on an 8x8 chessboard, the maximum number of bishops that can possibly be placed on the board is 14; adding an extra one will cause it to lie on a diagonal that was already covered by another bishop, so those two will attack each other. Indeed, we can place exactly 14 bishops on the board so that none of them attack each other (see Munem's solution for a possible configuration). Thus, our answer is $\boxed{14}.$