Black book 6
Let A B C be a given triangle.Points D and E are on sides A B and A C respectively and point F is on line segment D E .Let A B A D = 0 . 5 , A C A E = . 6 , D E D F = . 8 Let area of Δ B D F = Δ 1 , area of Δ C E F = Δ 2 and area of Δ A B C = Δ
-
Δ Δ 1 is equal to P
-
Δ Δ 2 is equal to Q
Find 2 P + 1 0 Q .
Bones :Generalize it.
The answer is 0.88.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
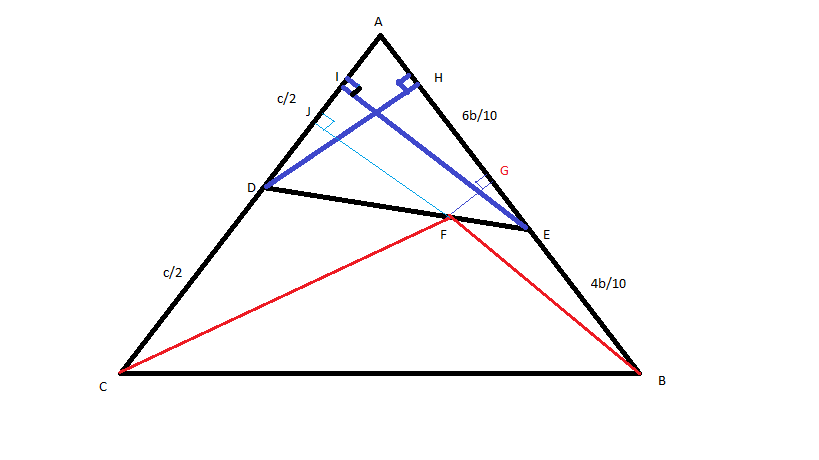
a , b , c a r e s i d e s o f t r i a n g l e o p p o s i t e t o A , B , C r e s p e c t i v e l y
AE= 1 0 6 b , EB= 1 0 4 b , AD=DC= 2 c The side lengths as shown in the figure can be found by ratios given.
△ = 2 1 c H ( h e r e H i s t h e h e i g h t o f △ A B C w i t h b a s e A B ) H = c 2 △ s i n A = b H = c b 2 △ E I = s i n A ∗ E A = c b 2 △ ∗ 1 0 6 b = 5 c 6 △ I n △ A D E , F J ∣ ∣ E I A p p l y i n g s i m i l a r i t y , u s i n g D F : F E = 8 : 2 F J = 1 0 8 E I = 2 5 c 2 4 △ ( F J i s h e i g h t o f △ D F C ) △ 1 = 2 1 ∗ 2 c ∗ F J = 2 5 6 △ .
In the very similar way, we find the area of triangle(EFB) from FG. After finding FG from DH.
△ 2 = 2 5 △ .
P = △ △ 1 = 2 5 6 Q = △ △ 2 = 2 5 1
2P+10Q=0.88.
We're done!
For generalization the same steps can be followed through variables.
Generalization was bit bulky with six variables : )
Can u please post the solution in L A T E X
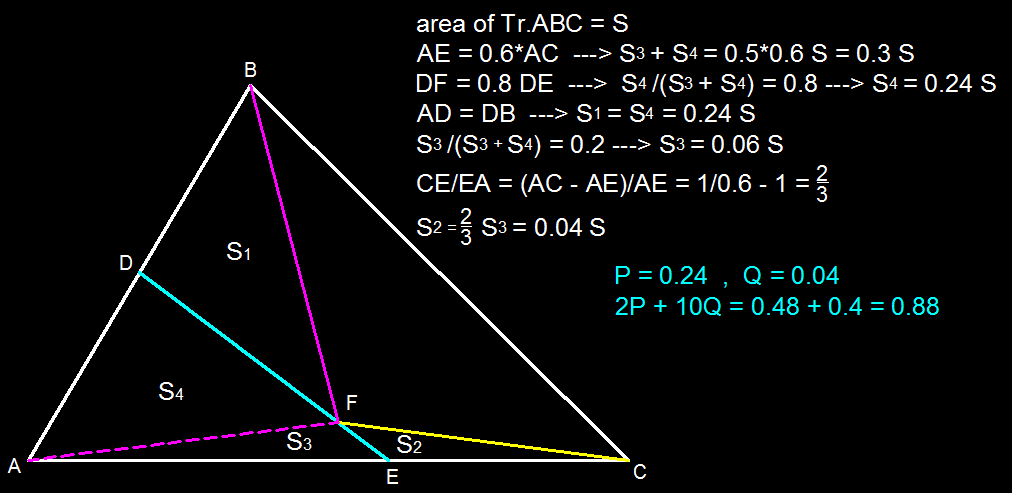
All triangle pairs with common vertex have, their area are simply in proportion to their base. Let area be shown as [XYZ]. Take Δ [ A F E ] = k . S o Δ [ A D F ] = . 2 . 8 k = 4 ∗ k Δ [ A D E ] = 5 k ; Δ [ D B F ] = . 5 . 5 ∗ Δ [ A D F ] = 4 ∗ k . D e l t a [ E F C ] = . 6 . 4 ∗ Δ [ A F E ] = 3 2 ∗ k Δ [ A D E ] Δ [ A B C ] = . 5 ∗ . 6 k 1 ∗ 1 k ∴ Δ [ A B C ] = . 3 5 k = 3 5 0 k ∴ P = 3 5 0 k 4 k = 2 5 6 . ∴ Q = 3 5 0 k 3 2 k = 2 5 1 . 2 P + 1 0 Q = 2 5 1 2 + 2 5 1 0 = 0 . 8 8