Black Box Impedance Sleuthing

Electricity and Magnetism Level 4

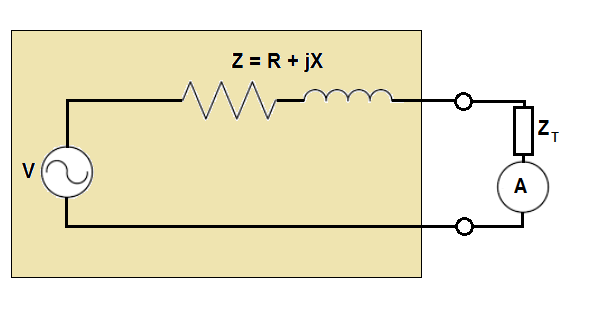
Suppose there is a box containing an ideal sinusoidal AC voltage source (RMS magnitude of V V ) in series with a resistance R R and an inductive reactance X X (for a total complex impedance Z = R + j X ) Z = R + jX) . The circuit is incomplete, and a pair of terminals are brought outside the box. Aside from the availability of the terminals, the box is closed and its contents are inaccessible.

You want to find out the values of the resistance and inductive reactance, so you devise a clever strategy to determine them. You take three measurements, each time connecting an ideal AC ammeter in series with a test impedance Z T Z_T and connecting the series combination across the box terminals.

For the first measurement, Z T Z_T is a perfect short-circuit with zero impedance, and the measured RMS current magnitude is V α \Large{\frac{V}{\sqrt{\alpha}}} .

For the second measurement, Z T Z_T is a 1 Ω 1 \Omega resistance, and the measured RMS current magnitude is V α + 5 \Large{\frac{V}{\sqrt{\alpha+5}}} .

For the third measurement, Z T Z_T is a 1 Ω 1 \Omega inductive reactance, and the measured RMS current magnitude is V α + 9 \Large{\frac{V}{\sqrt{\alpha+9}}} .

What is the value of R + X R + X ?

Note: In electrical engineering, the letter ′ ′ j ′ ′ ''j'' is commonly used to denote − 1 \sqrt{-1} , since the letter ′ ′ i ′ ′ ''i'' is commonly used to represent current.


The answer is 6.

Steven Chase by Steven Chase , 37, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

4 solutions

Guilherme Niedu
Jan 11, 2017

Relevant wiki: RLC Circuits (Alternating Current)

The three measures are:

∣ V R + j X ∣ = V α \large \Big | \frac{V}{R+jX} \Big| = \frac{V}{\sqrt{\alpha}}

∣ V ( R + 1 ) + j X ∣ = V α + 5 \large \Big | \frac{V}{(R+1)+jX} \Big| = \frac{V}{\sqrt{\alpha+5}}

∣ V R + j ( X + 1 ) ∣ = V α + 9 \large \Big | \frac{V}{R+j(X+1)} \Big| = \frac{V}{\sqrt{\alpha+9}}

So:

∣ R + j X ∣ = α \large |R + jX| = \sqrt{\alpha}

∣ ( R + 1 ) + j X ∣ = α + 5 \large |(R+1) + jX| = \sqrt{\alpha+5}

∣ R + j ( X + 1 ) ∣ = α + 9 \large |R + j(X+1)| = \sqrt{\alpha+9}

Or:

( i ) R 2 + X 2 = α \large (i) R^2 + X^2 = \alpha

( i i ) R 2 + 2 R + X 2 = α + 4 \large (ii) R^2 + 2R + X^2 = \alpha + 4

( i i i ) R 2 + X 2 + 2 X = α + 8 \large (iii) R^2 + X^2 + 2X = \alpha + 8

Plugging ( i ) (i) on ( i i ) (ii) :

2 R + α = α + 4 \large 2R + \alpha = \alpha + 4

R = 2 \large \color{#3D99F6} R = 2

Plugging ( i ) (i) on ( i i i ) (iii) :

2 X + α = α + 8 \large 2X + \alpha = \alpha + 8

X = 4 \large \color{#3D99F6} X = 4

Then:

R+X=6 \large \color{#3D99F6} \fbox{R+X=6}

4 Helpful 0 Interesting 0 Brilliant 0 Confused
Arjen Vreugdenhil
Jan 16, 2017

The rms current satisfies I r m s = V r m s ∣ Z ∣ , I_{rms} = \frac{V_{rms}}{|Z|}, where Z Z is the impedance of the entire circuit. In the three cases given, Z = R + X j Z = R + Xj , Z = ( R + 1 ) + X j Z = (R + 1) + Xj , and Z = R + ( X + 1 ) j Z = R + (X+1)j , respectively.

For the first situation, we have ∣ Z ∣ = α |Z| = \sqrt{\alpha} , so that ∣ Z ∣ 2 = R 2 + X 2 = α . |Z|^2 = R^2 + X^2 = \alpha. For the second measurement, we have ( R + 1 ) 2 + X 2 = α + 5 , (R+1)^2 + X^2 = \alpha + 5, and subtracting out the first equation this simplifies to 1 + 2 R = 5 1 + 2R = 5 or R = 2 R = 2 . Finally, R 2 + ( X + 1 ) 2 = α + 9 , R^2 + (X+1)^2 = \alpha + 9, which yields 1 + 2 X = 9 1 + 2X = 9 or X = 4 X = 4 .

The required answer is R + X = 6 R + X = \boxed{6} .

2 Helpful 0 Interesting 0 Brilliant 0 Confused
Chew-Seong Cheong
Jan 11, 2017

The first current measurement:

I 1 = V α V ∣ R + j X ∣ = V α ∣ R + j X ∣ = α R 2 + X 2 = α ⟹ R 2 + X 2 = α \begin{aligned} I_1 & = \frac V{\sqrt \alpha} \\ \frac V{|R+jX|} & = \frac V{\sqrt \alpha} \\ |R+jX| & = \sqrt \alpha \\ \sqrt{R^2+X^2} & = \sqrt \alpha \\ \implies R^2+X^2 & = \alpha \end{aligned}

Similarly for the second and third current measurements and we have:

{ R 2 + X 2 = α . . . ( 1 ) ( R + 1 ) 2 + X 2 = R 2 + 2 R + 1 + X 2 = α + 5 . . . ( 2 ) R 2 + ( X + 1 ) 2 = R 2 + X 2 + 2 X + 1 = α + 9 . . . ( 3 ) \begin{cases} R^2+X^2 = \alpha & ...(1) \\ (R+1)^2+X^2 = R^2+2R+1 + X^2 = \alpha + 5 & ...(2) \\ R^2+(X+1)^2 = R^2 + X^2 + 2X + 1 = \alpha + 9 & ...(3) \end{cases}

Therefore, we have { ( 2 ) − ( 1 ) : 2 R + 1 = 5 ⟹ 2 R = 4 ⟹ R = 2 Ω ( 3 ) − ( 1 ) : 2 X + 1 = 9 ⟹ 2 X = 8 ⟹ X = 4 Ω \begin{cases} (2) - (1): & 2R+1 = 5 & \implies 2R = 4 & \implies R = 2\Omega \\ (3) - (1): & 2X+1 = 9 & \implies 2X = 8 & \implies X = 4\Omega \end{cases}

⟹ R + X = 2 + 4 = 6 \implies R+X = 2+4 = \boxed{6}

2 Helpful 0 Interesting 0 Brilliant 0 Confused

i refuse to believe it's level 5 , :( now the solution is convention , given in others ' solution :\

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...