Black box
A circuit with 5 resistors of 1 Ω is put into a black box, so that we don't know how the resistors are connected. If you measure the equivalent resistance between the points A and B, you get that it's 3 5 Ω . The equivalent resistance between the points A and C is 3 8 Ω . There are two possible equivalent resistances between B and C. One of those resistances is 1 Ω . What is the possibility for the other resistance between the points B and C in Ω ?

The answer is 1.66667.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
With at most 5 resistors of 1 Ω , there is only one way to create a circuit with equivalent resistance is 3 5 Ω and a circuit with 3 8 Ω , which show in this image .
Therefore, there is only one possible circuit for the circuit in the black box, which is also shown in this image .
Therefore, the equivalent resistance between B and C is 3 5 Ω
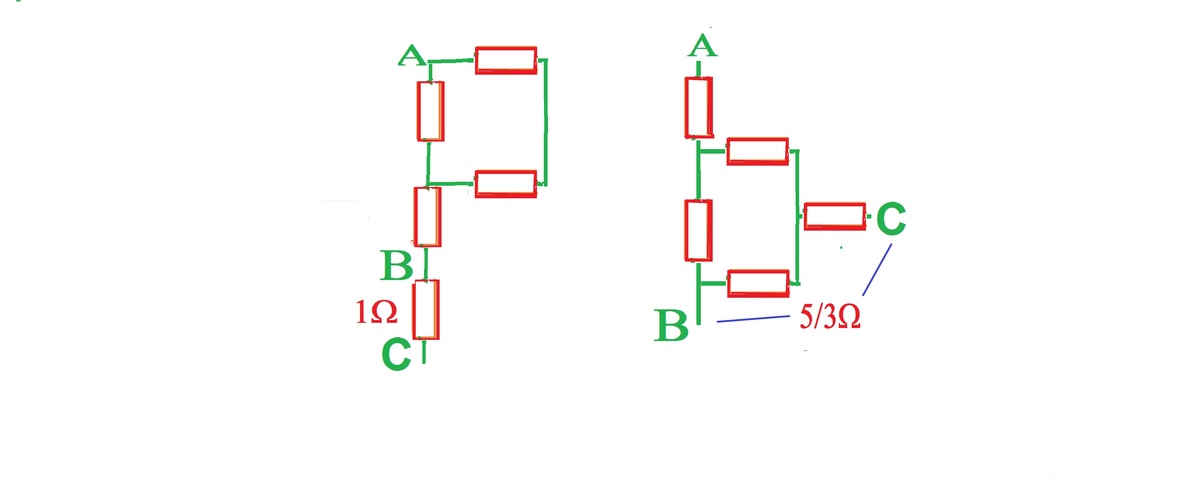 For AB and AC same resistance there are two ways to connect . In one BC is
1
Ω
. and in the other BC is
3
5
Ω
. as shown.
For AB and AC same resistance there are two ways to connect . In one BC is
1
Ω
. and in the other BC is
3
5
Ω
. as shown.
R {AB} = \frac{5}{3} >1 so we can obtain that there is one resistor connected in series with the other set of resistors. The value of that set is \frac{5}{3} -1 = \frac{2}{3}. It is clearly that this set contains (2 resistors in series, the joint of them is D) parallel with one resistor. R {AC}= \frac{8}{3} 1Ohm greater than R {AC}. Therefore, the possible arrangement is that D is connected with C by one resistor. So, R {BC} is ((R+R)//R)+R = \frac{5}{3}
Since we don't know how the resistors are connected, we can do some trial. We may see that:
R A B = 3 5 = 1 + 3 2 = 1 + 1 + 2 1 1 = 1 + 1 + 1 1 + 1 1 1 1
R B C = 3 8 = 1 + 1 + 1 + 1 1 + 1 1 1 1
From above equation we can obtain this circuit. Hence, R B C = 3 5 ≈ 1 . 6 6 6 7 Ω