Block and Spring

Classical Mechanics Level 3


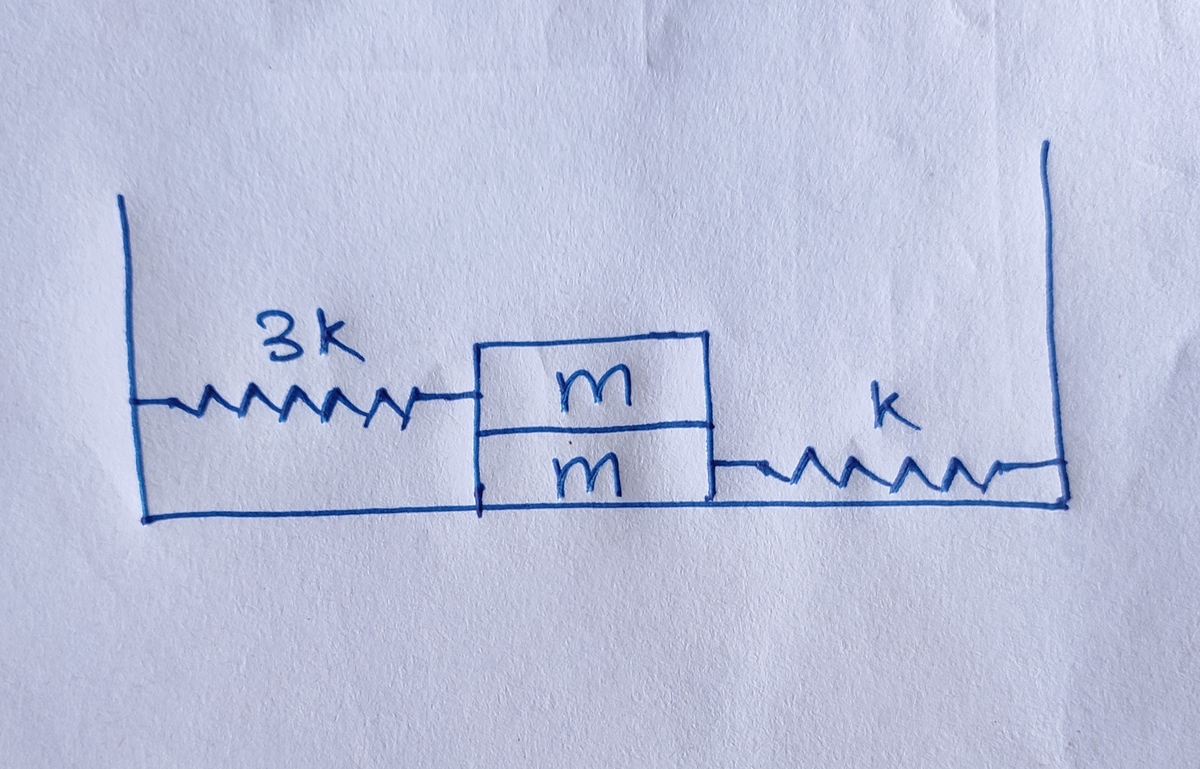
When the arrangement shown is in equilibrium, the spring on the right is stretched by an amount x 0 . x_{0}.

Coefficient of static friction between the blocks is μ \mu and the horizontal floor is frictionless. Both the blocks have equal mass m m and the horizontal floor is frictionless. Both the blocks have equal mass m m and force constants of the spring are 3 k 3k and k k as shown in the figure.

The maximum amplitude of oscillations of the blocks along with the springs that do not allow them to slide on each other is in the form α μ m g k + β x 0 , \frac{ \alpha \mu mg}{k} +\beta x_{0}, where the acceleration of free fall is g g .

What is the sum of constants α + β \alpha + \beta .


The answer is 0.

Talulah Riley by Talulah Riley , 18, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

What is to be submitted as the answer is not given. Let us assume that it is α + β α+β .

Initially it is not told whether the spring on the left has any stretch or not.

Equilibrium condition is : Applied force ≤ \leq limiting value of friction force . It is not told whether the system impends motion initially (the two forces are equal). Let us assume that they are equal : k x 0 = μ m g kx_0=\mu mg

Let the maximum stretch of the right spring, which determines the amplitude required, be x x . Then

3 k ( x − x 0 ) + μ m g = k x ⟹ 3k(x-x_0)+\mu mg=kx\implies

x = 3 x 0 2 − μ m g 2 k x=\dfrac {3x_0}{2}-\dfrac {\mu mg}{2k}

So α = − 1 2 , β = 1 2 , α=-\dfrac 12,β=\dfrac 12, and α + β = 0 α+β=\boxed 0 .

1 Helpful 1 Interesting 1 Brilliant 0 Confused

Nice, that's how I did it too.

Krishna Karthik - 7 months, 1 week ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...