Block on Incline (2)
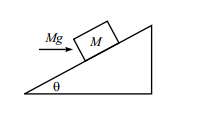 A block of mass M rests on an fixed incline plane of angle
θ
.
A horizontal force of magnitude Mg is applied on the block, If the coefficient of static friction of the incline be
0
.
5
. For what ranges of
θ
will the block still remain at rest?
A block of mass M rests on an fixed incline plane of angle
θ
.
A horizontal force of magnitude Mg is applied on the block, If the coefficient of static friction of the incline be
0
.
5
. For what ranges of
θ
will the block still remain at rest?
Note : The answer is of the form a ≤ t a n θ ≤ b Find a b
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Decompose the forces into normal and parallel axes (to the inclined plane). We find that the forces along the plane is ∣ M g ( sin θ − cos θ ) ∣ and that pressing against the wedge is M g ( sin θ + cos θ ) Identify the limiting cases where the whole friction is either acting downwards along the plane or upwards along. We will get the equations as sin θ + cos θ sin θ − cos θ = ± 2 1 Thus we get tan θ = 3 , 3 1 Hence the answer 1
so what is wrong with my solution?
mg/cosA=mg.sinA+0.5mg.sinA
and then i found tanA is about 0.89. i thought that a and b are 0 and 1. This is only solution what school tought me. I can't understand where did you got that equation mostly the 'use' of coefficient static friction. Would you explain it more detailer?
Hey Himanshu, how do we attach an image with the solution?
how can we split the forces in its components.. can anyone explain it graphically..
The normal force F N on the block is given by: F N = M g ( s i n θ + c o s θ ) Therefore, the frictional force: F = 0 . 5 M g ( s i n θ + c o s θ ) The resultant force on the block is given by: F R = M g ( c o s θ − s i n θ ) The block is at rest if: F N ≤ ∣ F R ∣ ⇒ 0 . 5 M g ( s i n θ + c o s θ ) ≤ ∣ M g ( s i n θ + c o s θ ) ∣ ⇒ 0 . 5 ( s i n θ + c o s θ ) ≥ ⎩ ⎪ ⎨ ⎪ ⎧ c o s θ − s i n θ s i n θ − c o s θ ÷ c o s θ ⇒ 0 . 5 ( t a n θ + 1 ) ≥ ⎩ ⎪ ⎨ ⎪ ⎧ 1 − t a n θ t a n θ − 1 ⇒ ⎩ ⎪ ⎨ ⎪ ⎧ 1 . 5 t a n θ ≥ 0 . 5 1 . 5 ≥ 0 . 5 t a n θ ⇒ 3 1 ≤ t a n θ ≤ 3 ⇒ a b = 3 1 × 3 = 1