Block, Ramp, and Spring

A block of mass $m$ is positioned on a right-triangular ramp of vertical height $h$ and mass $M$ . A spring with force constant $k$ and natural length $L_0$ is attached between the ramp and the wall as shown. All surfaces are smooth. The block can slide along the ramp surface, and the ramp can slide along the floor. The ramp makes an angle $\theta$ with respect to the horizontal. There is a downward gravitational acceleration $g$ .

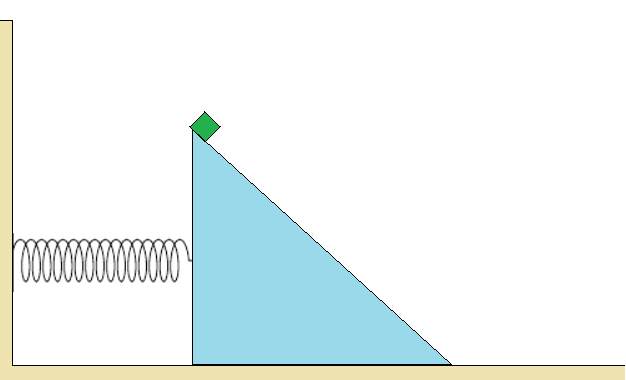
At time $t = 0$ , the block is at the top of the ramp, and the spring is at its natural length $L_0$ . Both the block and the ramp are initially at rest. The block slides down the ramp over time.

The block reaches the floor at time $t_f$ . Let $L'$ be the minimum spring length over the period of time between $t = 0$ and $t = t_f$ . Enter your answer as the following quantity:

$\large{\lfloor 100 \, ( L' + t_f) \rfloor}$

Details and Assumptions:
Here, "m" can mean "meter", or it can refer to the block mass, depending on the context
- $(m , M) = (1 \, kg, 2 \, kg)$
- $(k , L_0) = (50 \, N/m, 1 \, m)$
- $(h , \theta) = (2 \, m, \frac{\pi}{6} \, rad)$
- $g = 10 \, m/s^2$
- $\lfloor \cdot \rfloor$ denotes the floor function
- During the period of interest, the block remains fully in contact with the ramp, and the ramp remains fully in contact with the floor.
- The block's size is negligible