Blocks inside blocks!
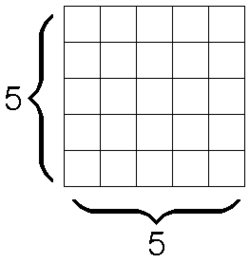The above figure is a
square which is formed of
small squares. Let the number of squares and rectangles in the above figure be
and
respectively. Find
.
Hint: Every square is a rectangle but vice versa is not true.
The answer is 280.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Each rectangle can be uniquely determined by 2 vertical lines and 2 horizontal lines. There are 6 possible vertical lines and 6 possible horizontal lines.
Hence the number of rectangles is ( 2 6 ) ∗ ( 2 6 ) = 2 2 5 rectangles.
Next, we count the number of squares. It is helpful to consider the possible positions of the top left hand corner of each square to count the number of squares. By casework,
1x1 squares: 25
2x2 squares: 16
3x3 squares: 9
4x4 squares: 4
5x5 squares: 1
The total number of squares is 1 + 4 + 9 + 1 6 + 2 5 = 5 5 .
Hence m + n = 2 2 5 + 5 5 = 2 8 0