Blow of sight
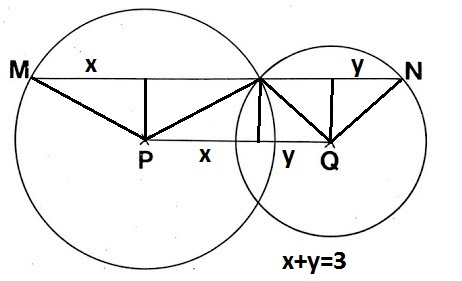
Two circles with respective centers P and Q intersect with each other, as shown below. Line segment M N is parallel to P Q and goes through one of the intersection points.
If P Q = 3 , what is M N ?
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
28 solutions
What if Q gets very close to P then the above solution doesn't work anymore, i think?
Log in to reply
If Q gets very close to P then the circles no longer intersect so MN can't go through the intersection point and the problem cannot then be asked
Log in to reply
As the lines get infinitely close, the circles approach touching in only 1 point and MN as the sum of diameters is twice PQ as the sum of radii so the answer still holds.
I agree with Ralph. But if they just get close and you can still draw two skinny triangles the proof should hold.
Man you better not use the paint app to draw these stuff 😂😂
I extended PQ to the far sides of each circle and dropped vertical lines from M and Q to P1 and Q1 and saw that MP1Q1NM is a rectangle. P1P = X and Q1Q = Y, so the answer is 2x+2y = 2 (x+y) = 6.
Log in to reply
Yes. Note that in general MN=2XPQ (= 6 in this case) for any configuration of the circles that intersect at two points and in one point if the smaller circle is moved to the right tangent to the large circle.
me too, I can't believe it
all i did was compare lengths and they looked the same to my eye....................
That's how I did it. Nice job. I'm wondering, though, if there is a more elegant solution.
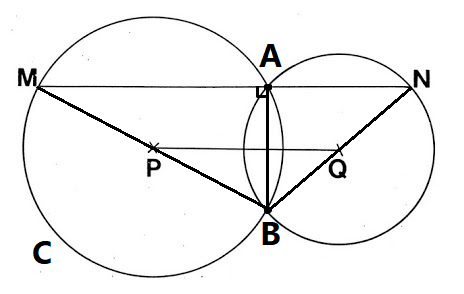
∡ M A B = 9 0 ∘ , so arc M C B must be a semicircle, and therefore M B is a diameter. The same reasoning can be applied to N B . Therefore, when connecting these two segments, △ M N B and △ P Q B are created, and △ M N B ≃ △ P Q B .
Since P B is a radius of P and M B is a diameter, the scale factor between the two triangles is 2 , so M N = 3 ∗ 2 = 6 .
Bast solution by you.. Thanks
How do you know that angle MAB is 90°?
Log in to reply
Because the angle MAB delimits the arc of half circle
Log in to reply
Also, when we have two circles that overlap, the line (in this case vertical) between the two points at which the circles overlap is always straight, unless otherwise stated. One can stretch the straight vertical line and form a 90° angle with another line that is laying flat across any horizontal point of the circles.
but you didn't prove that extending NQ would indeed go through the other intersection point of the two circles.
Log in to reply
Adding AQ and AP radii in does that for you with alternate/corresponding angles, isosceles triangles and the perp. bisector to the chord. I drew them in before the AB chord and did it Zain's way too.
I proved that NB is a diameter of the circle, which implies that N, B, and Q are collinear.
I also thought this, but you posted answer faster than me
Consider the special case where the circles with centers P and Q are tangent, and the answer is obvious.
Additionally, you can also consider the case where the diameter of one of the circles is 0.
Many problems are easy to solve - if one assumes that there is a solution. Of course the mere fact that the question was asked does not guarantee that there is a single solution - but it sure suggests it.
Log in to reply
Plus the fact that there is no way to answer “depends” in the answer blank.... ;)
Yep this is exactly how I did it, pretty easy
I first saw the special case of equal radii, then tangent, then zero before constructing Zain's diagram to prove.
Is not so obvious.... you have assumed the law for tangent circles continues to apply when they are secant. Of course, your assertion is true, but special cases don't generally apply to construct more general laws.
Log in to reply
It is obvious, but only if someone is a visual thinker. It doesn't require complicated calculations, but not everyone thinks in this manner.
Log in to reply
Not everything obvious is true. That extrapolation he did needs to be backed up by formal math.
I use this solution as well, feels like cheating, since actually proving that the ratio will always hold when the circles intersect is not straightforward, but since the format of the question implies that, one can also argue that this is the clever shortcut solution.
Construct Perpendicular bisectors of the two chords and the correct (6) follows immediately.
Yes, that’s how I did it also! Even though it’s not rigorous it’s still nice 😊👍
Its actually so easy if you simplify it down to squares
Best solution posted ! Thanks mate xD
Ohhh very good
GOOD GRIEF!!! There are so many geometric "solutions", but the answer is intuitive. WHAT IF the intersecting points were ON PQ? The radius of Circle P plus the radius of Circle Q would be the length of PQ and MN would be an extension of PQ, also known as the DIAMETERS of Circles P and Q, or TWICE the length of PQ. THEREFORE MN = 2PQ is the base length equation, and MN = 6 where PQ = 3. DON'T MAKE IT SO HARD, PEOPLE!
I also thought of this approach. However, it assumes that the problem is correct - that MN is always the same length independent of the sizes of the circles.
An intuitive solution is examining the special case when the two circles are tangential. I know for a perfect solution you should be sceptical by not accepting the implicitly suggested rule that the length of the line segment MN is independent of the radii, and suspecting incomplete data in the problem.
I simply measured both lines to determine that MN was twice PQ
Think of a special case where the 2 circles are identical and just tangentially touch at one point. Then PQ = 2 R, R being the radius of the circles. Then, MN is colinear with PQ and its length is 2 (2R). This gives MN = 2*3 = 6!
Oops, sorry, I didn't see this, and posted a duplicate. Next time I will expand the view I promise :)
2x+2y=MN (equation 1), x+y=3 (equation 2). common factor: 2(x+y) =MN. (inserting equation 2 in 1): 2*3=MN, MN=6
PQ=3; MP+QN=3;MP+QN=PQ;2MP=3-PQ;2MP=3-3=0! => MP=0 , so MN = 6 because then the 2 circles are concentric.
You'll sometimes come across a problem like this, where if you trust the setters to know what they are doing you can solve it instantly on inspection. Notice that they haven't said anything about the distance between the lines MN and PQ, so it's reasonable to assume the answer does not depend on this distance. So make the distance zero, as others have said, when the circles are tangent and the lines are collinear. Then it's obvious that MN is twice PQ.
I used the theorem of intersecting lines
:
Let X 1 and X 2 be the intersection points of the two circles; X 1 lies on M N .
From symmetry, we see that P Q is a bisector of X 1 X 2 . Let R be the midpoint of X 1 X 2 , i.e its intersection with P Q .
Now consider the triangles M X 1 X 2 and P R X 2 . They are similar triangles (here we use the fact that M N is parallel to P Q ), with ratio X 1 X 2 : R X 2 = 1 : 2 . Thus M R : P R = 1 : 2 . Similarly, R N : R Q = 1 : 2 ; and so M N : P Q = 1 : 2 .
Conclusion: M N = 2 P Q = 2 ⋅ 3 = 6 .
I simply measured both parallel lines to determine that Line MN was twice line PQ.
Almost no math required. Line MN looked twice as long as line PQ.
1.5^2+1.5^2=x^2 x=2.12 3^2=1.5^2+x^2 x=2.59 2.59^2+2.59^2=x^2 x=3.67 MN=3.67+2.12=5.79 or fucking 6 !!!!!
If you regard the other intersection point of the circles as a vertex, R, than triangle PQR is similar to triangle MOR. Since line segment MR is the diameter of the circle to which MP is the radius, MR must be twice the measure of PR. (The same goes for OR and QR.) Since they share vertex R and are similar, triangle MOR is necessarily twice the size of triangle PQR, and so line segment MO is twice the length of line segment PQ.
Since the question says "as shown" I have to assume that the dimensions and angles are exact. Thus I just used a ruler to measure PQ on my screen (4.5cm) and then measured MN (9cm) and multiplied by the same scale factor (2/3).
If we increse the diameter of Q and decreese the diameter of P mantening the size of PQ, we will see the line MN decending to the center of the circules and and his size will be the sum of diametrr P and Q. And as we did, diameter P = Q, MN =6. Sorry about gramatic errors, I'm Brazilian.
As we connect the two intersecting points with a line we see that PQ cut it in the middle then for the suggested line from N through Q according to Thales' theorem it must end with its double which mean the diameter of the circle that would not intersect the line connecting the two intersecting points in a point other than the lower intersecting point that forms a triangle with the line MN and by applying Thales' theorem scale fraction it is clear that MN=2PQ=2(3)=6 😊
A very nice, very clear solution is this:
The intersection point will be denoted as T. Take PQ's midpoint, and take the line crossing it, perpendicular to PQ. T's reflection to the line will be called point S. Obviously, S is on MN.
Since P's reflection to the line is Q, PT's reflection is QS, PT=QS. But PT is the radius of the bigger circle, so QS=PM, therefore PQSM is a paralelogram, and MS=PQ. Same bway can be shown that QPSN is also a paralelogram, so SN=PQ.
MN=MS+SN=PQ+PQ=6
At tangency, the equation is PQ=R+r and MN=2PQ, giving a general equation of MN=2(R+r) where R is the radius of the left hand circle and r is the radius of the right hand circle.
Let's take an special case of the two intersecting circles, touching each other:
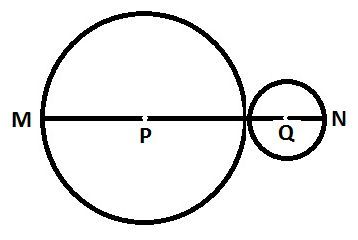 Now, if r1 and r2 are the radii of the circles, PQ = r1 + r2 = 3. Or in terms od diameters, d1/2 + d2/2 = 3 => d1+d2 = MN = 6
Now, if r1 and r2 are the radii of the circles, PQ = r1 + r2 = 3. Or in terms od diameters, d1/2 + d2/2 = 3 => d1+d2 = MN = 6
John Knox. The intersection of the circles is not fixed so the problem asks for a ratio or we can move the circles as long as they have a common point of intersection. By moving the second circle to the right so that it is tangent to the first circle it becomes obvious that MN equals 2XPQ. In this instance or configuration of circles PQ equals 3, the sum of the radii of the two circles, while it is obvious from this configuration that MN equals PQ plus the sum of the radii of the two circles or 6. The fact that MN equals 2XPQ holds as long as the circles have a common point although I have not given a rigoruos proof. Proof anyone?
Let P be the center of coordinates with coordinates (0,0).. The coordinates of Q are (3,0). Let (x,y) be the coordinates of the intersection.point R. Then MR = 2x and RN = 2(3-x). so MN = MR + RN = 6. Ed Gray
Let R1 be the radius of the left circle and R2 be the radius of the right circle. Let a be the length of the horizontal distance between the overlapping circles on PQ. We can see that MN = 2(R1-a/2) + 2(R2-a/2) = 2(R1 + R2 -a) However, PQ = R1 + R2 -a = 3 Therefore, MN = 2 x PQ = 6
The answer can be easily arrived at by using the converse of midpoint theorem. Draw diameters of both circles intersecting the POI of both circles and lying on MN. By applying the coverse of midpoint theorem ( PQ parallel MN) (PQ bisects common chord) Thus, MN=2PQ
As PQ = 3, I thought of the special case where the centers are tangent. With this in mind, the answer is obvious.
Add an identical circle the size of Q on the other side of P that is also 3 units away. Construct a line that is perpendicular to PQ that passes through both intersection points. Repeat for the circle on the other side. Similar constructions can also be done on the other side of Q with a circle of size P. These constructions show that |MN| = 2|PQ|.
I was calculating like crazy, but the answer was right in front of my nose the whole time