Blue area
 There is a square and four circles, each with the same radius equal to the side of the square, and their centers are the vertices of the square.
Find the ratio of the shared area to the area of the square.
There is a square and four circles, each with the same radius equal to the side of the square, and their centers are the vertices of the square.
Find the ratio of the shared area to the area of the square.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
very nice solution.I upvote your solution.
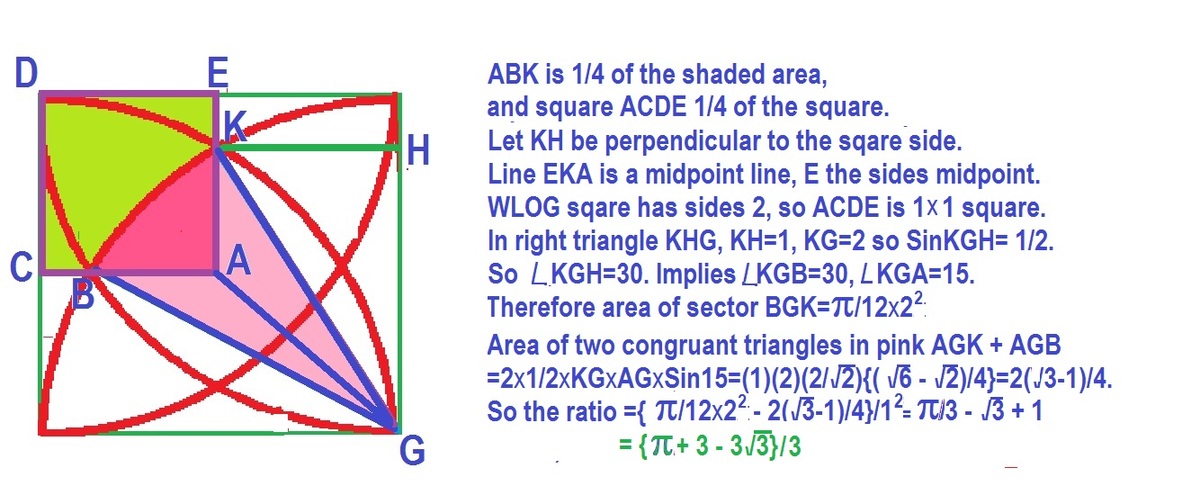 The sketch explains how to find the ratio for one fourth. For the hole too it will have the same ratio.
The sketch explains how to find the ratio for one fourth. For the hole too it will have the same ratio.
From the diagram on the left, you can see that the blue area is the area of the square minus 4 of the shaded region on the left. Therefore, we want to find the area of the shaded region.
From the diagram on the right, we know that:
Shaded area = Area of Sector AED - Area of Segment AE
Furthermore, we know that:
Area of Segment AE = Area of Sector BAE (with center B) - Area of Triangle ABE
Now, let the sides of the square (and the radius of the circles) be a
We know that AE is the radius of Sector ABED, therefore AE = a
We know that BE is the radius of Sector BAEC, therefore BE = a
Therefore, triangle ABE is an equilateral triangle with sides a
We can then calculate everything out now:
Area of Segment AE
= Area of Sector BAE (with center B) - Area of Triangle ABE
= 3 6 0 6 0 π a 2 − 2 1 a 2 sin 6 0 ∘ = 6 π a 2 − 4 3 a 2 = 1 2 2 π − 3 3 a 2
Area of shaded region
= Area of Sector AED - Area of Segment AE
= 3 6 0 3 0 π a 2 − 1 2 2 π − 3 3 a 2 = 1 2 π a 2 − 1 2 2 π − 3 3 a 2 = 1 2 3 3 − π a 2
Blue area (shared area)
= Area of square - 4 × Area of shaded region
= a 2 − 4 × 1 2 3 3 − π a 2 = 3 3 + π − 3 3 a 2
The ratio of shared area to area of square
= a 2 ( 3 3 + π − 3 3 a 2 ) = 3 π + 3 − 3 3