Blue Bayou
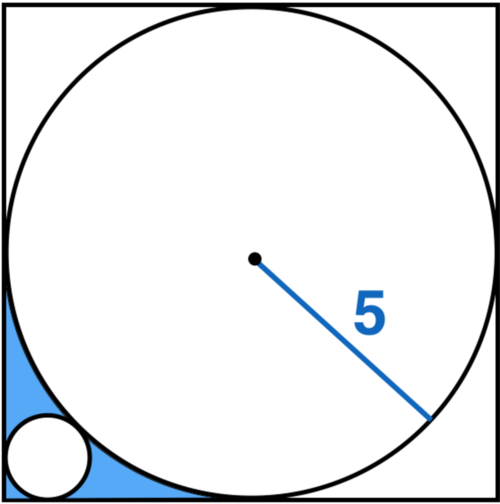 A circle is inscribed in a square as shown above. A smaller circle is drawn tangent to two sides of the square and externally tangent to the inscribed circle. Find the area of the blue shaded region to two decimal places.
A circle is inscribed in a square as shown above. A smaller circle is drawn tangent to two sides of the square and externally tangent to the inscribed circle. Find the area of the blue shaded region to two decimal places.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
14 solutions
very nice solution
How do you know that AB = AC?
Log in to reply
Log in to reply
I assume that point G is the point of tangency between the small circle and the large circle, point H between the small circle and the bottom of the square, and point I between the small circle and the right side of the square.
Thanks for replying :D
Simpler answer: Because ABC is a right triangle and angle ACB is 45 degrees.. Therefore, ACB is isosceles with AC = AB.
But, the last equation results to two possible answers. It could also be 15+10sqrt(2).
Log in to reply
That would be 29.14…, which is far too large to fit in the space allowed. We know that r must be less than 1 to fit between the corner of the square and the tangent point on the large circle.
Excellent.......
Nice. I solved it this same exact way too.
did the same way
How did you get 3.06417? Doing the math gets ≈ 3.05305
1 2 3 4 5 6 7 8 9 |
|
Wow. Great solution. I wasn't able to see this simple method of solving the question and instead used a much longer version that took me a long time.
Mnie wyszło około=1,98
how do you approximate that without a calculator???
First, find the area A which includes the area of blue region and small circle.
As there is a square which has length 10m, and a circle which has radius 5m,
Second, find the radius of small circle, x,
draw a triangle like this,
By Pythagoras' Theorem,
So, Area of small circle,
very nice solution
didn't understand the Pythagoras theorem portion how the equation forms?
Log in to reply
Split the lower left quarter of the square into a right-angled triangle. The hypotenuse (half of the diagonal of the square) is 5 2 + 5 2 = 5 0 So this is the distance from the centre of the square/circle all the way down to the bottom. The hypotenuse of the lower left triangle that he's drawn is then 5 0 take the radius of the large circle take the radius of the small circle, which, by simple Pythagoras, equals x 2 + x 2 So in the end you get x 2 + x 2 = 5 0 − 5 − x or alternatively the way he did it.
Infinite geometrical progression of circle diameters for the win !!
I don't understand what you mean. Where is infinite G.P.????
Log in to reply
Notice that the smaller circle can be inscribed in a square of its own with four blue corners and an even tinier circle tucked in the lower-left tiny blue corner. I believe Susant is saying that the ratio of the radius of the large circle to the small circle of the problem is equal to the radius of the small circle to the radius of the even smaller circle. You continue this to an infinite number of ever-smaller circles; and the sum of the radii is 5sqrt2. If x is the ratio, I believe the equation would be 5sqrt2 = 5 + 5x +5x^2 +.... or sqrt2 = 1/(1-x). Solve for x to get the radius of the small circle in the problem, which is 5x. The area is (pi)25x^2.
Wouldn't we have to know the font and the font size of the "5" and the thickness of the radius that was drawn, to be able to say exactly the blue area on the diagram. :-P
For those (like me) not sharp enough to see some of the hidden relationships, here's a rigorous solution.
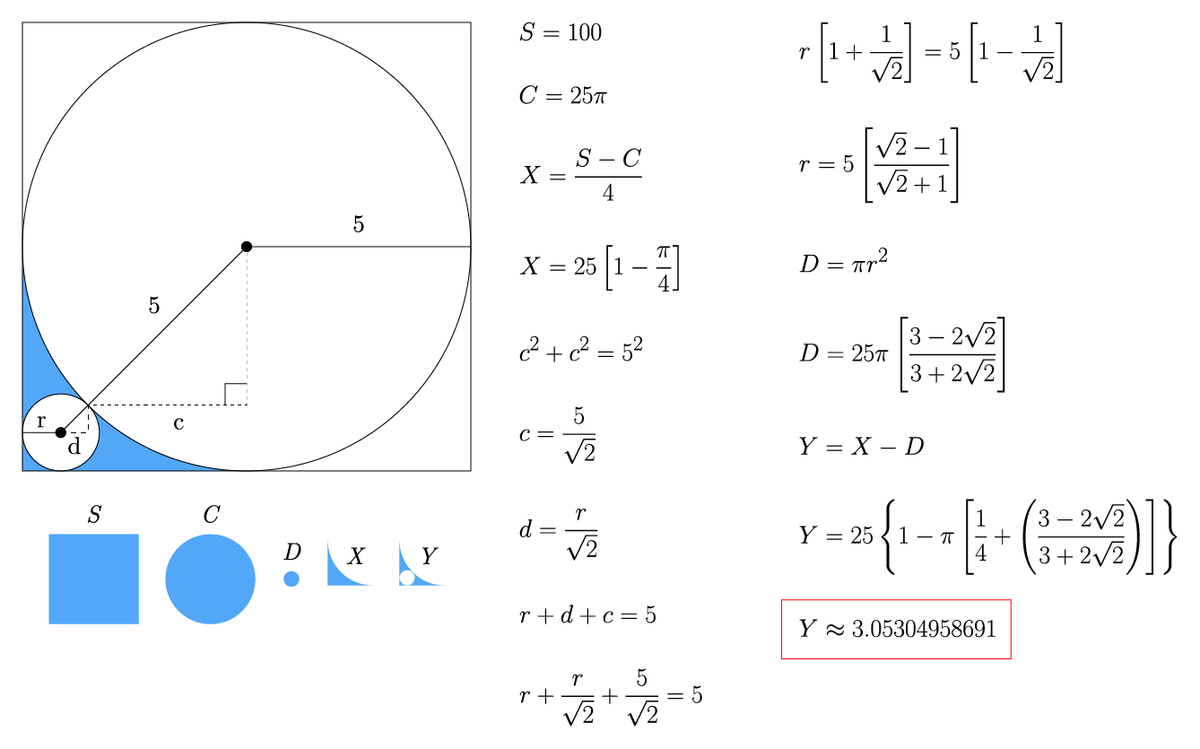
The blue area + little circle area is 4 1 0 2 − 5 2 π
Second, the radius of little circle is R and one way of find it is:
 A
T
=
X
+
2
R
=
5
2
−
5
A
T
=
X
+
2
R
=
5
2
−
5
2 2 = R + X R
Solving this system of equations we get R = 2 + 2 1 0 − 5 2 ⇒ the area of little circle is ( 2 + 2 1 0 − 5 2 ) 2 × π
∴ blue area is 4 1 0 2 − 5 2 π − ( 2 + 2 1 0 − 5 2 ) 2 × π ≈ 3 . 0 5
çok güzel.RAMİREZ
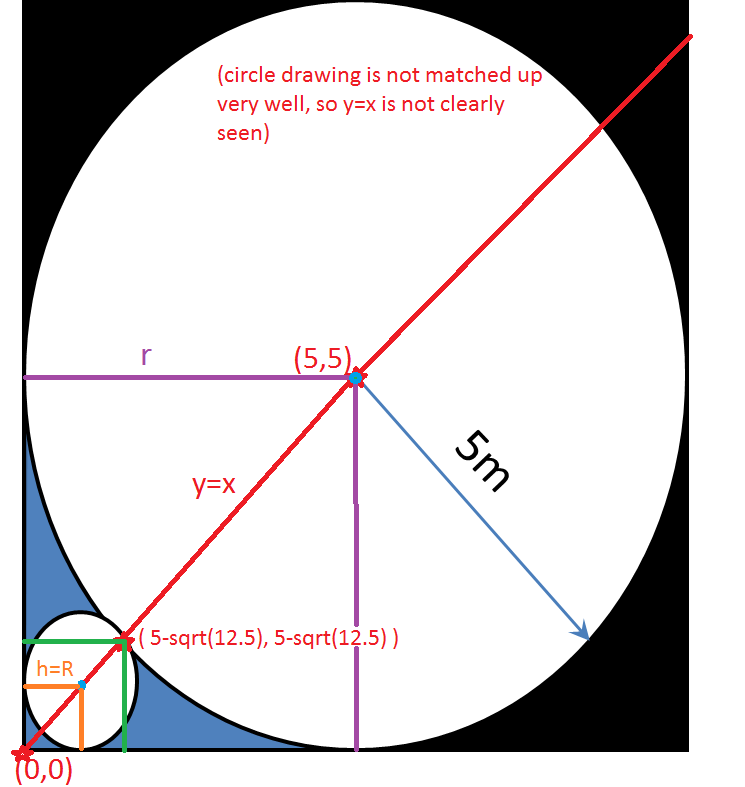 Consider the bottom left corner the origin. (x-5)^2 +(y-5)^2 =25 describes the inner circle. The line y=x intersects the centers of the large and small circles. The place where y=x intersects the large circle nearest the origin is also the point that the large and small circle share. y=x, therefore, 2(x-5)^2 =25.
Consider the bottom left corner the origin. (x-5)^2 +(y-5)^2 =25 describes the inner circle. The line y=x intersects the centers of the large and small circles. The place where y=x intersects the large circle nearest the origin is also the point that the large and small circle share. y=x, therefore, 2(x-5)^2 =25.
x=(5-sqrt(12.5)), which is also y. Since the center of the smallest circle also lies along y=x, the same symmetry may be applied to it. let R be the radius of the small circle. (x-h)^2 +(y-k)^2 =R^2.
h=k.
y=x.
h=k=R.
The radius is half the height of the circle, or half the distance across the circle, through the center, in any direction. 2(5-sqrt(12.5)-R)^2=R^2. R= (5(sqrt(2)-1)/(sqrt(2)+1)). Now consider the purple square in my version of the picture, of area r^2 (25 units). Subtract away the portion of the large circle that is inside of it. The area of the large circle inside the purple box is 25(pi/4). 25-25(pi/4) or 25(1-(pi/4)). Then subtract out the area of the small circle. The area of the small circle is (pi * (5(sqrt(2)-1)/(sqrt(2)+1))^2 ).
This is approximately 5.365045915 - 2.311996328.
The closest answer is 3.05 m^2
Let r be the radius of the small circle.
Then we have two equal expressions for the length of the diagonal from the center of the large circle to the bottom left corner:
5 2 = 5 + r + r 2
Solving for r :
r = 5 ( 2 + 1 2 − 1 )
The area of the blue shaded region is:
A b l u e = 4 A s q u a r e − A l a r g e c i r c l e − A s m a l l c i r c l e = 4 1 0 2 − π ( 5 ) 2 − π r 2 ≈ 3 . 0 5 3
The solution found by Mas Mus is much more insightful and elegant, but I will still include mine that is based on logic, which is not always the shortest way, but helps analysing various situations.
The side of the circumscribed to the circle square is double the size of the circle radius, so its area SA =
1
0
2
= 100. The area of the circle is CA = π
5
2
= 78.5. Their difference is SA - CA = 100 - 78.5 = 21.5. This devided by 4 gives us the area comprising the blue area and the small inscribed circle, i.e. 21.5 =
5.37
(1). We need to subtract the area of the small circle.
The distance from the center of the big circle to one of the corner of the square is is the hypotenuse of the right triangle formed by two sides equal to the radius of the big circle (or half the side of the square):
d
2
=
5
2
+
5
2
= 50 and d =
5
0
= 7.07. So, the distance from touch point of the two circles to the corner of the square = 7.07 - 5 = 2.7. This consists of the diameter of the small crcle plus an extra portion, let's all it 'x', from the circle to the corner of the square.
Let r be the radius of that circle. We have two equations:
a) 2r + x = 2.07 => x = 2.07 - 2r
b)
r
2
+
r
2
=
(
r
+
x
)
2
=> (from the right triangle, similar to the big one desceibed above) =>
r
2
=
x
2
+ 2rx (after expansion and simplification).
Replacing 'x' in (b) with its equivalent found in (a), we get
r
2
= 4.28 - 4.14r (after expansion and simplification) or
r
2
+ 4.14r - 4.28 = 0
. This is a quadratic equation that can be solved using the formula for quadratic equations:
r =
2
−
4
.
1
4
+
1
7
.
1
4
+
4
∗
4
.
2
8
. This gives us 0.857. So the area of the small circle is 3.14*
0
.
8
5
7
2
= 2.31. Subtracting from tha value we found in (1), we get 5.37 - 2.31 =
3.06
Let us call the radius of the large circle
R
, and the radius of the small circle
r
. The area of the outer square is then
S
:
=
(
2
R
)
2
, the area of the large circle is
C
:
=
π
R
2
, and the area of the small circle is
c
:
=
π
r
2
. The area of the blue region is then simply
A
=
4
S
−
C
−
c
=
4
4
−
π
R
2
−
π
r
2
.
By considering the isosceles right triangle, whose hypotenuse is
2
times longer than its legs, we obtain
r
in terms of
R
as follows (cf. the figure below):
r
=
2
+
1
2
−
1
R
=
(
2
−
1
)
2
R
.
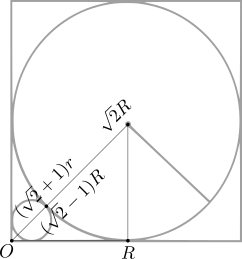 Thus, the area in question may be expressed in terms of the radius of the larger circle as a quadratic function:
A
(
R
)
=
(
1
−
4
π
−
π
(
2
−
1
)
4
)
R
2
≈
0
.
1
2
2
1
2
2
R
2
⇒
A
(
5
)
≈
3
.
0
5
3
0
5
□
Thus, the area in question may be expressed in terms of the radius of the larger circle as a quadratic function:
A
(
R
)
=
(
1
−
4
π
−
π
(
2
−
1
)
4
)
R
2
≈
0
.
1
2
2
1
2
2
R
2
⇒
A
(
5
)
≈
3
.
0
5
3
0
5
□
I can see that people like to do this the hard way, with "exact" numbers of pi and such.(like using pi=3.141592... instead of approximations) so I'll show you how I'd do this without a calculator.
First off I want to find how long the side of the square is, and that is the same as the diameter of the larger circle, which is 5 2=10 I'd also like to know the approximate diameter of the small circle which I can approximate to be the remaining part of the hyphothenuse of the triangle with the sides of the radius of the large circle. So the diameter of the small circle is √(5²+5²)-5= =√(2 5²)-5=5√2-5 and which a approximation of √2=1.4 means that d=5*1.4-5=7-5=2 which means the small circle has a radius of 1.
Now to find the blue area. The area of the square is 10²=100, and the area of the large circle is 5² π, and I'll approximate π=3 which makes the area to be 5² 3=25 3=75. Therefore the area of the ramaining part of the square is 100-75=25 which makes one part of it be 25/4≈24/4=6 and then we take that minus the area of the small circle which is 1² π=1*3=3. So the area of the blue part is approximately a little larger than 3 which makes 3.05 the closest answer. Therefore it is 3.05, and that's how you do this without a calculator.
area of the large square = 100
area of the large circle = 25 PI = 78.53975
area of one of the 4 corner "triangles" = (square - circle) / 4 = 5.36506
diagonal from center to corner of large square = (pythagorean) sqrt (50) = 7.07107
difference of diagonal less large radius = 2.07107
ratio of difference to large radius = 0.41421
r = radius of small circle
diagonal = 7.07107 = 5 + 2.41421 r
solve for r = 0.85786
area in blue = corner "triangle" less area of small circle = 5.36506 - PI * r * r = 3.05307
X= radius of the big circle & R=radius of the small circle R = X × 1 + C o s 4 5 1 − C o s 4 5 Area of the blue region = X 2 × ( 1 − 4 π ) − π × R 2 in this case X=5m so R=0.8579m and the Area of the blue region=3.0535 s.m.
Radius of the smaller circle = 5*(sqrt(2)-1)/((sqrt(2) + 1) = 0.8579
Area of the shaded Region = Area of the Square with side = 5^2 = 25 - Area of quarter circle = pi 5^2/4 - Area of smaller circle = pi 0.8579^2 = 3.0528
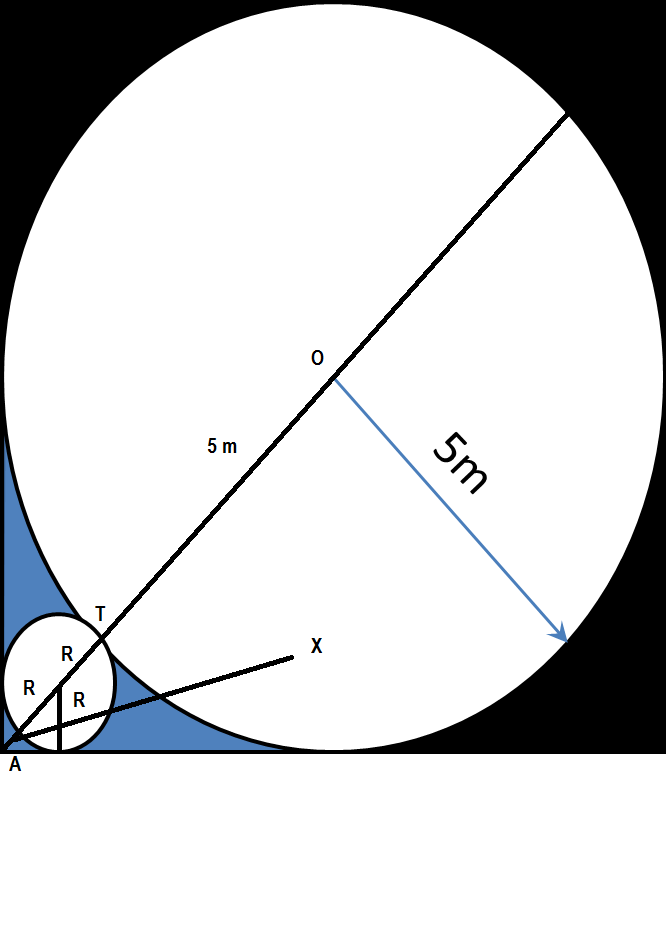
Let r is the radius of small circle. The △ A B C is a right triangle with A B = A C = 5 − r and B C = 5 + r . Now, using Pythagorean Theorem we have 2 5 + 1 0 r + r 2 r 2 − 3 0 r + 2 5 ( 5 + r ) 2 = 5 0 − 2 0 r + 2 r 2 = 0 = 2 ( 5 − r ) 2
Solving the last equation to get r = 1 5 − 1 0 2 . Finally, the area of the shaded region is
5 2 − 4 1 × π × 5 2 − π × ( 1 5 − 1 0 2 ) 2 ≈ 3 . 0 6 4 1 7