Blue circle puZZle
 interesting geometry problem
Hello genius minds, this is Mind Your Concept welcoming you to this math's paradox. I am Swaroop Dora.
interesting geometry problem
Hello genius minds, this is Mind Your Concept welcoming you to this math's paradox. I am Swaroop Dora.
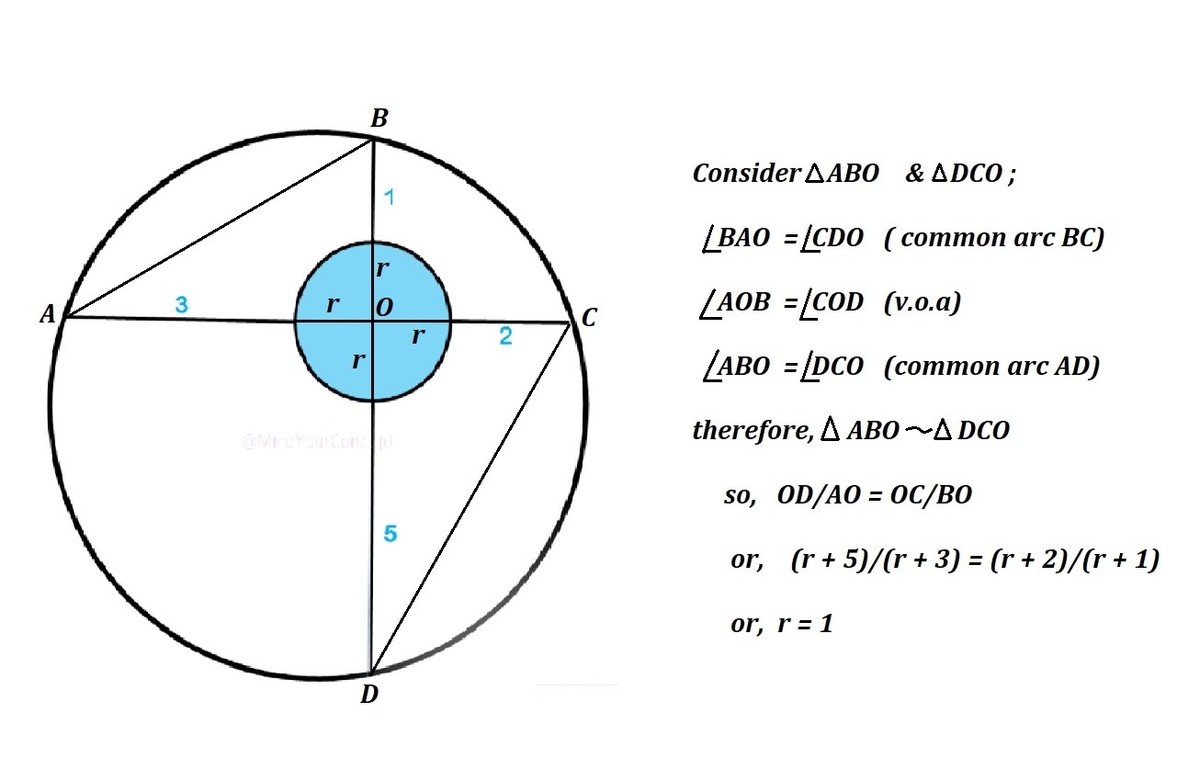
Question: A arbitrary blue circle is chosen inside a big circle. The distance of blue circle from big circle in north, south, east and west directions are 1, 5, 2, and 3 respectively. What is the radius of the blue circle?
I found this puzzle interesting because it can be fun if we ask taking the big circle as earth and blue circle as moon. Giving required distances we can ask for radius of moon.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.