Blue + Green = Turquoise
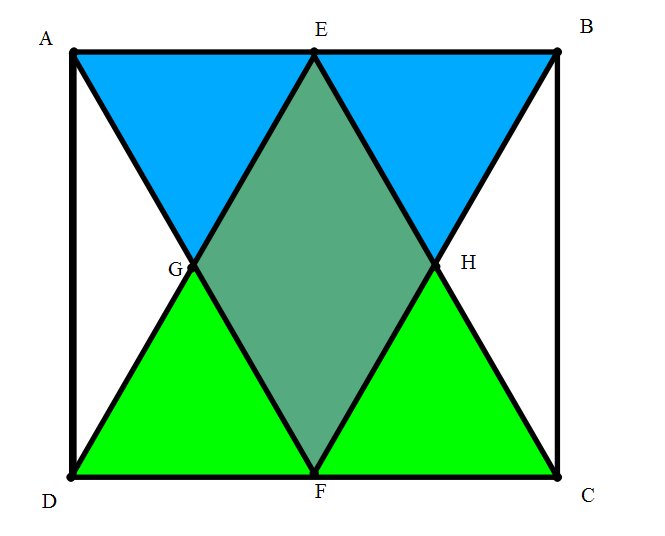 ABCD is a unit square, with E the midpoint of AB and F the midpoint of CD. Draw the isosceles triangles ABF and DEC, which intersect at points G and H. What is the area of the
diamond-shaped
quadrilateral EGFH?
ABCD is a unit square, with E the midpoint of AB and F the midpoint of CD. Draw the isosceles triangles ABF and DEC, which intersect at points G and H. What is the area of the
diamond-shaped
quadrilateral EGFH?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The diamond shape is composed of two non-overlapping triangles each with base length 2 1 and height 2 1 . Thus their combined area is 2 ∗ ( 2 1 ) 3 = 4 1 .