Blue or Yellow plus Red
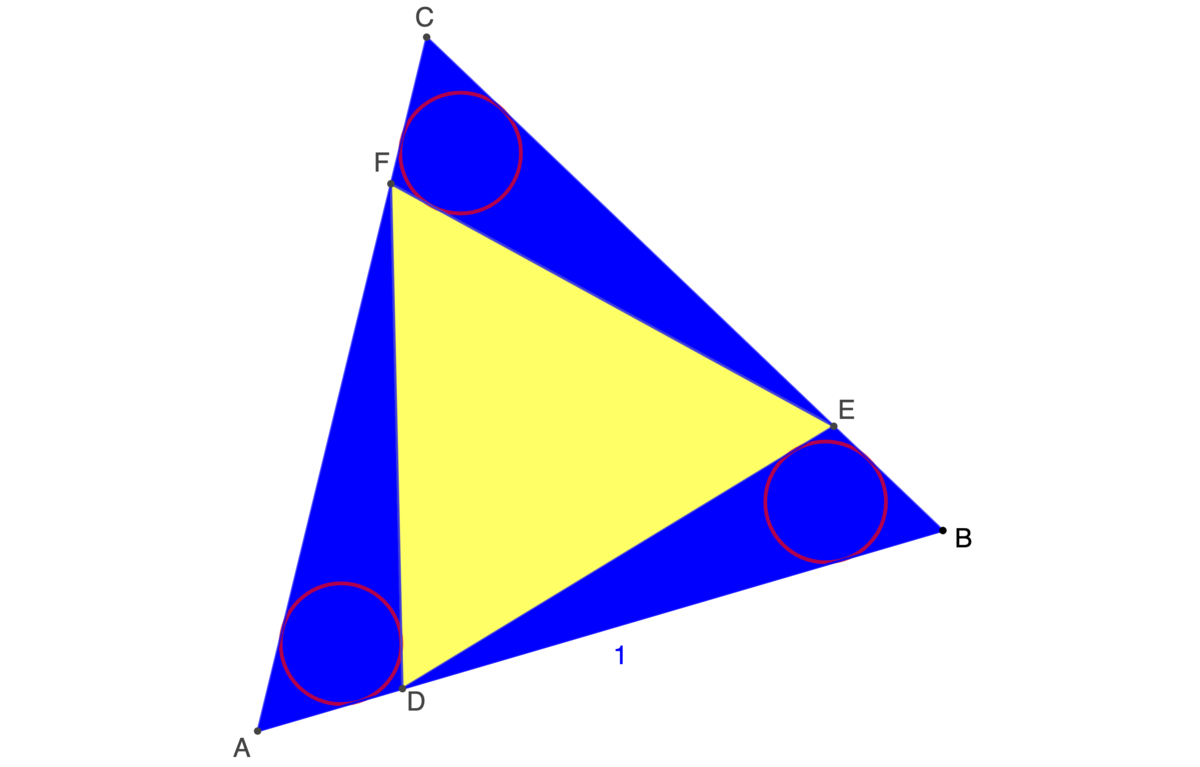
The figure shows a yellow equilateral triangle, , inscribed inside a unit equilateral triangle, .
If the blue area is the same as the yellow area, what is the radius, , of the red incircles inscribed in the three subtriangles? If , submit .
The answer is 23.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Since the yellow area and blue area are equal, the area of the yellow equilateral triangle is half that of the unit equilateral triangle, and the area of one of the blue triangle is 6 1 that of the unit equilateral triangle or A = 6 1 ⋅ 4 3 = 8 3 1 .
Since the yellow equilateral triangle is half that of the unit equilateral triangle, its side length is 2 1 . Let us consider one of the blue triangles △ B D E . Then D E = 2 1 . Let B E = a ; then A D = a and D B = 1 − a . The semiperimeter s = 2 2 1 + a + 1 − a = 2 2 1 + 1 .
The radius of a red circle
r = s A = 4 3 ( 2 1 + 1 ) 1 = 4 ⋅ 3 ( 2 + 1 ) ( 2 − 1 ) 2 ⋅ 3 ( 2 − 1 ) = 1 2 2 3 − 6
The required answer is a + b + c + d = 2 + 3 + 6 + 1 2 = 2 3 .