Blue or Yellow
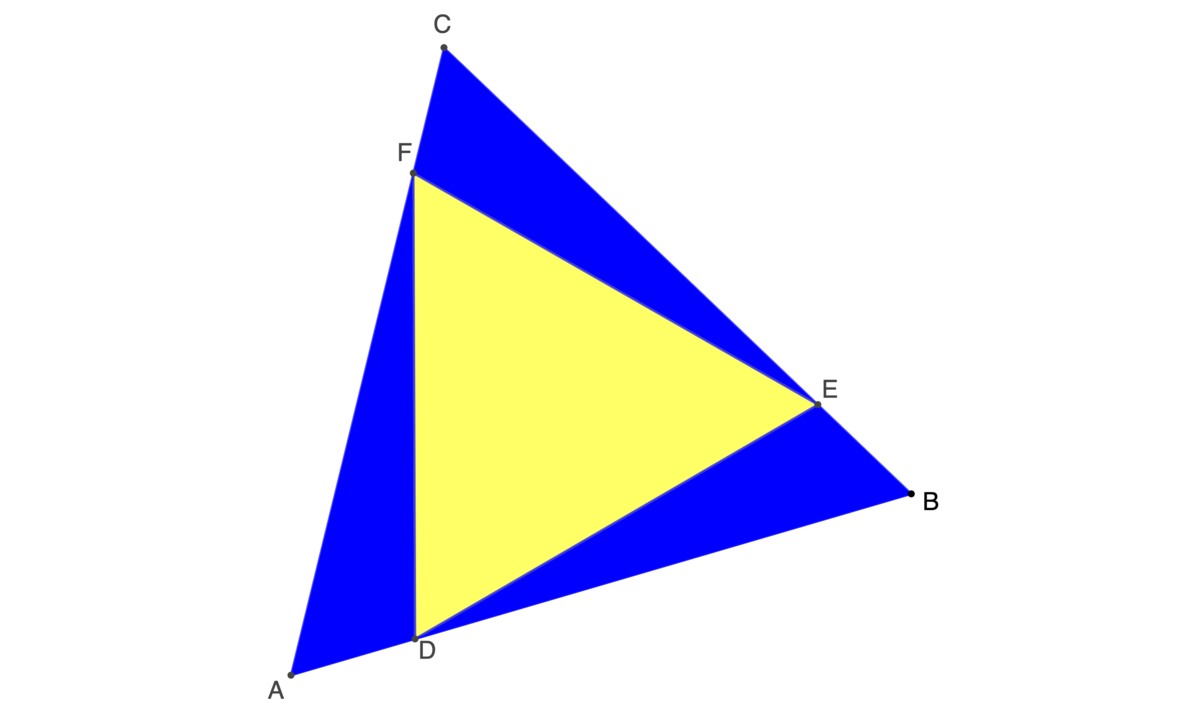
The figure shows a yellow equilateral triangle, , inscribed inside a larger equilateral triangle, .
. Which is the larger area, blue or yellow?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the side length of the larger equilateral triangle be 1 . Then A D = 5 1 and D B = 5 4 . By cosine rule ,
D E 2 D E 2 = E B 2 + D B 2 − 2 ⋅ E B ⋅ D B ⋅ cos B = 2 5 1 + 2 5 1 6 − 2 ⋅ 5 1 ⋅ 5 4 ⋅ cos 6 0 ∘ = 2 5 1 7 − 2 5 4 = 2 5 1 3 Note that E B = A D = 5 1
Since the area of an equilateral triangle is directly proportional to the square of its side length, the area of the yellow equilateral triangle is 2 5 1 3 that of the large equilateral triangle. This means the blue area is 2 5 1 2 that of the large equilateral triangle. Hence yellow area is larger than the blue area.