Blue/Red

△ A B C is isosceles with A B for its base. Cevians A E and F B are drawn to the corners of the inscribed blue square. The three red squares are congruent. What is the ratio of the area of the blue square to the area of one of the red squares?
The answer is 9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Assuming Side of red square to be 1 is a bit tricky..
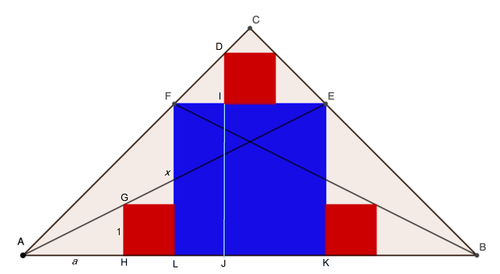
Let the side length of the red square and blue square be 1 and x respectively, and A H = a . Since △ A G H and △ A E K are similar, we have:
G H A H = E K A K ⟹ a = x a + 1 + x ⟹ a = x − 1 x + 1
Similarly, △ A F L and △ A D J are similar,
F L A L x a + 1 x a + 1 2 ( a + 1 ) ( x + 1 ) 2 a x + 2 a + 2 x + 2 2 a + 2 x + 2 x − 1 2 ( x + 1 ) + 2 ( x + 1 ) x − 1 2 2 x ( x − 3 ) x = D J A J = 1 + x a + 1 + L J = 1 + x a + 1 + 2 x − 1 = 2 ( x + 1 ) 2 a + x + 1 = 2 a x + x 2 + x = 2 a x + x 2 + x = x 2 + x = x ( x + 1 ) = x − 2 = x 2 − 3 x + 2 = 0 = 3 Note that a = x − 1 x + 1 Since x + 1 > 0 Since x > 0
U too assumed it to be 1 Isn't it just a specific case??
Log in to reply
The answer is a ratio. It is perfectly okay to assume any length to be 1. If we assume the side length of the blue square to be 1 and look for the side length of the red square a . Then a = 3 1 and the answer is 9 . If we assume the side length of the red square to be x , then we will find that the side length of the blue square be 3 x . So there is no difference it is just that we save a lot on keying in x here and there.
Label the diagram as follows, and let the side of the blue square be b , the side of the red square be 1 , and A G be p :
Since △ A J G ∼ △ A E I , J G A G = E I A I , or 1 p = b p + 1 + b , which rearranges to p = b − 1 b + 1 .
Since △ A F H ∼ △ F L K , F H A H = L K F K , or b p + 1 = 1 2 1 ( b − 1 ) , which rearranges to p = 2 1 b ( b − 1 ) − 1 .
That means p = b − 1 b + 1 = 2 1 b ( b − 1 ) − 1 , which rearranges to b ( b − 3 ) ( b + 1 ) = 0 , and solves to b = 3 for b > 0 .
Therefore, the ratio of the area of the blue square to the area of one of the red squares is 1 2 b 2 = 9 .