Find The PRO Angle
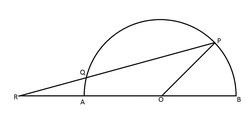 O is the center of the semicircle. If RQ = BO and the measure of
∠
BOP is 60 (in degrees), then find the measure of
∠
PRO (in degrees).
O is the center of the semicircle. If RQ = BO and the measure of
∠
BOP is 60 (in degrees), then find the measure of
∠
PRO (in degrees).
The answer is 20.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
There is no indication that Angle BOP is on the midpoint of the circle. Your problem lack details. There is a possibility that angle BOP is not exactly in the mid point but just inside the circle. Try to put more details on your illustrations.
Log in to reply
Thanks for telling me my mistake..... I have edited my problem. I will take care of these mistakes from next time.
more detalis means less thinking...the correct answer is 20 degrees..its not hard to solve ....just a matter of observation..
O is Centre of semi circle.......
this is also my same object
why BOP is 3x
Log in to reply
∠ AOQ + ∠ POQ + ∠ BOP = 180. ∠ AOQ = x, and ∠ POQ = 180 - 4x. Putting the values of ∠ AOQ and ∠ POQ, we get x + 180 - 4x + ∠ BOP = 180. Then ∠ BOP = 180 - 180 + 4x - x which is equal to 3x.
my way is wayyyyyyyyyyyy easier .yours a bit complicated
O that is very neat, thank you for a good solution, I just remembered that it was the trisection construction and thence guessed 20. Your detailed solution revised me how, thank you.
hahaha I'm good at guessing
Nicely done
As other answers have explained, △ Q R O is isosceles with Q R = Q O . Let x denote ∠ Q R A and ∠ Q O A (they are congruent).
There is a very useful identity on the angles formed by two secant lines in a circle. Secant angle identity
Applying the identity: x = 2 1 ( ∠ P O B − ∠ Q O A )
x = 2 1 ( 6 0 ∘ − x )
x = 2 0 ∘
nice
Let the desired angle be 't'. So by sine rule of the triangle poq which is isosceles we get that sin(60-t)=sin2t.So we get that t is 20 or 120 degrees. But t can not be obtuse.so t=20 degrees....
BOP is an equilateral triangle; let angle OPR=y; angle PRO=x; x+y=60 by exterior angle theorem(1); triangle POQ is isosceles and hence angle PQO = y; in triangle QRO 2x+180-y = 180 -> y = 2x; hence 3x=60 by (1) -> x = 20
join OQ. now, RQ=BO (given) also BO=OQ= Radius .: RQ=OQ join OQ=OP=RADIUS NOW APPLYIN ANGLE SUM PROP AND PROPERTIES OF ISOSCELES TRIANGLE ONE CAN SOLVE ANGLE PRO=20
There is an isosceles triangle RQO since QO=BO=RQ.
The angles opposite the equal sides are also equal, so angle QRA = angle QOA = arc AQ (central angle), let them be x.
To find the angle (x) formed by two secant lines that intersect in the exterior of a circle is... one half of the difference of the measure of the intercepted arcs.
x = 1/2 (60 - x)
x = 20
Simply join the "point O" with "point Q", then it will make a isoceles triangle and the angles <ORQ=<ROQ. Then name these angle with any given name let θ . Then you know that the angle <QOR will be 120- θ . Then simply find the chord length QR since by then you would know the angle inscribed by the chord. After that you would know the length of segment RP wich will RQ+QR. Then by using sine formula, one can easily solve for the given angle θ .
well it was a question with lack of information..even though i solved it s=r€ is the answer compare and get it ,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,, let oA=oB=rQ=m=RA,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,s=r€ in OPB ......................WE GET..........>S=m60 ,,,,,,,,,,,now in RAQ,,,,,,,,,,,,,,,s=r€,,,,,,,,,,,,,,,,,,,,>>>>.s=3m€,,,,,,,,,,,,, ,,,,,,,,,,,,,,,now comparing s.........................3m€=m60.
>>>>>>>>>>>>>.€=20
First of all, Join OQ. Now, BO = RQ = OQ (radius of same circle). So, ∠ QRO = ∠ QOR. Let them be x.
Applying exterior angle property, ∠ PQO = ∠ QRO + ∠ QOR = 2x. And as OQ = OP, ∠ PQO = ∠ QPO = 2x. And using angle sum property, ∠ POQ = 180 - 4x.
Now AB is a Straight line. So, ∠ AOQ + ∠ QOP + ∠ BOP = 180. And we conclude that ∠ BOP = 3x. But ∠ BOP = 60 and this enables us to find the value of x = 20.
So, ∠ PRO = 2 0 .