Bohr's orbit

Classical Mechanics Level 3

An electron with charge $e$ revolves around a nucleus of an element with atomic number $Z.$ Find the value of $Z$ when $47.2 \text{ eV}$ of energy is needed to excite the electron from the second Bohr's orbit to the third.

6 8 4 5

1 solution

Jonathan Xian Kuan Chee
Dec 30, 2014

Firstly, let's convert $47.2eV$ into joules. This can be done so using the formula, title title

Where $V$ is the voltage, $W$ is the work done in joules and $q$ is the charge of the electron, which is about $1.602\times { 10 }^{ -19 }C$ .

Then we may have to formulate Bohr's equation for energy by combining together the Rydberg formula and Planck's law.

title title AND $title$ title

Which leads us to this result,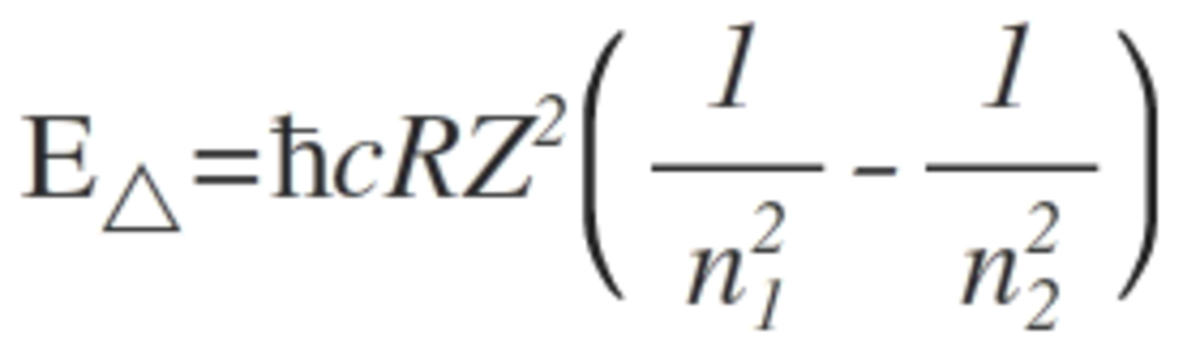

Where ${ E }_{ \triangle }$ is the energy change, $Z$ is the atomic number of the element, $R$ is the Rydberg constant, $h$ is the planck's constant, $c$ is the speed of light and $n$ will be the principal quantum numbers of the orbitals. Substituting the values yield a value close to $5$ which is the answer.

Bohr's orbit

1 solution

0 pending reports