Boinga, boinga, boinga goes the ball

Classical Mechanics Level 5

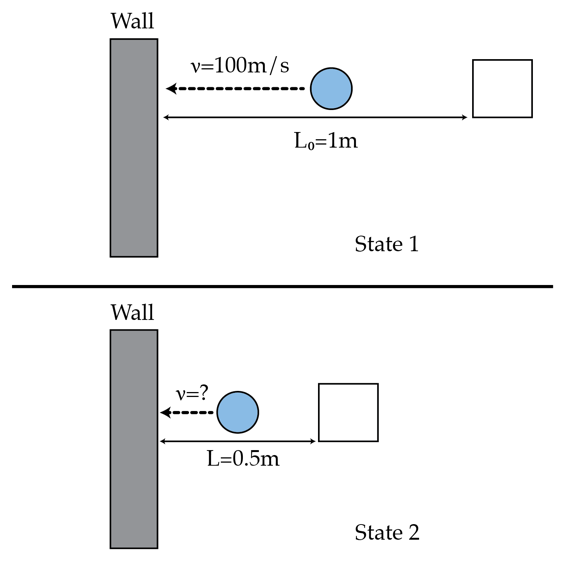
Sometime, even with only a very slow motion, you can still create a big change in a classical mechanics system. Consider the motion in 1 dimension of a ball between a wall (which is fixed) and a block (which is moveable). The distance between the block and the wall is L o = 1 m L_o=1~m and the speed of the ball is very large v o = 100 m / s v_o=100~m/s . The ball collides perfectly elastically with the block and the wall.

Let's move the block slowly to reduce the distance between it and the wall. Estimate the speed of the ball in meters-per-second when the distance is L = 0.5 m L=0.5~m

Details and assumptions

Neglect the size of the ball


The answer is 200.

David Mattingly by David Mattingly

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

David Mattingly Staff
May 13, 2014

The force we need to act on the block in order to move it is F = d p / d t = 2 m v 2 L / v = m v 2 L F=dp/dt=\frac{2mv}{2L/v}=\frac{mv^2}{L} . As you move the block by the distance d L dL , you give the energy d E = − F d L = − m v 2 d L L dE=-FdL=-\frac{mv^2dL}{L} to the system, and actually it will become the increase of the ball's kinetic energy d E = d K = d ( m v 2 2 ) = m v d v dE=dK=d(\frac{mv^2}{2})=mvdv :

m v d v = − m v 2 d L L ⇒ d v v = − d L L ⇒ ln ⁡ v v o = ln ⁡ L o L ⇒ v = v o L o L = 200 ( m / s ) mvdv=-\frac{mv^2dL}{L} \Rightarrow \frac{dv}{v}=-\frac{dL}{L} \Rightarrow \ln{\frac{v}{v_o}} = \ln{\frac{L_o}{L}} \Rightarrow v=v_o\frac{L_o}{L}=200(m/s)

5 Helpful 0 Interesting 1 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...